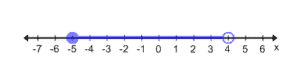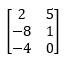Algebra 1 Help | Free Algebra 1 Lessons & Practice Problems

Go through the lessons and practice problems below to help you learn Algebra 1 and excel in school. We’ll track your progress and help you identify your strengths and weaknesses. Our Algebra 1 lessons is available to everyone, but you need to create an account in order to access the practice questions and track your progress.

Algebra 1: 01-Introduction to Algebra

A025 - Verbal to Algebraic Expressions
100.00% Review
A026 - Verbal to Algebraic Equations
Go >
A027 - Declaring Variables
Go >
A074- Order of Operations
Go >
A075-Order of Operations with Substitution
Go >
A079- Adding & Subtracting Real Numbers
Go >
A080- Multiplying & Dividing Real Numbers
Go >
Alg2/T CC 02 - Properties of Real Numbers
Go >
A081-Distributive Property
Go >
A082-Finding the Solution to an Equation
Go >

Algebra 1: 02-Solving Equations

A016 - Solving One-Step Equations
Go >
A017 - Solving Equations
Go >
A083-Multi-Step Equations
Go >
A084-Multi-Step Equations (Variable on Both Sides)
Go >
A020 - Linear Equations
Go >
A021 - Solving Proportions
Go >
A062-Complex Proportions
Go >
A085- Percents
Go >
A086- Percent Change
Go >

Algebra 1: 03-Solving Inequalities

A087-Graphing Inequalities
Go >
A088-Solving Inequalities Using Addition or Subtraction
Go >
A089- Solving Inequalities Using Multiplication & Division
Go >
A018 - Solving Inequalities
20.00% Review
A071- Compound Inequalities
Go >
A090-Solving Compound Inequalities
Go >
A091 - Absolute Value Equations
60.00% Review
A092 - Absolute Value Inequalites
Go >

Algebra 1: 04-Functions

A094- Using Graphs to Relate two Quantities
60.00% Review
A095- Patterns and Linear Functions
Go >
A096- Patterns and Nonlinear Functions
Go >
A097- Graphing a Function Rule
Go >
A098- Writing a Function Rule
Go >
A099- Formalizing Relations and Functions
90.00% Review

Algebra 1: 05-Linear Functions

A100- Slope
Go >
A037 - Slope of the Line Given Two Points
Go >
A038 - Equation of a Line, Given Slope and Y-Intercept
Go >
A102-Equation of a Line (Slope-Intercept Form)
Go >
A103- Equation of a Line (Point- Slope Form)
Go >
A143- Equation of a Line, Given a Point and Slope
Go >
A039 - Equation of a Line Given Point and Slope
Go >
A104-Equation of a Line (Standard Form)
Go >
A105-Equations of Parallel and Perpendicular Lines
Go >
A106- Scatter Plots and Trend Lines
Go >
A107-Graphing Absolute Value Functions
Go >

Algebra 1: 06-Systems of Equations and Inequalities

A048 - Solving a System of Equations Graphically
Go >
A108-Solving a System of Equations Graphically
Go >
A051 - Solving a System of Equations Using Substitution
Go >
A109- Solving a System of Equations with Substitution
Go >
A050 - Solving a System of Equations Using Elimination
Go >
A110- Solving a System of Equations using Elimination
Go >
A111- Applications of Linear Systems (Systems of Equations)
Go >
A055 - Word Problems: Systems of Equations
Go >
A056 - Word Problems: System of Equations II
Go >
A112-Graphing Linear Inequalities
Go >
A113- Systems of Linear Inequalities
Go >
A053 - Solving a System of Inequalities
Go >

Algebra 1: 07-Exponents and Exponential Functions

A002- Positive Exponents
Go >
A003 - Negative Exponents
Go >
A004 - Multiplying Terms That Have Exponents
Go >
A005 - Dividing Terms That Have Exponents
Go >
A114-Graphs of Exponential Functions
Go >
A069 - Exponential Growth
Go >
A070- Exponential Decay
Go >

Algebra 1: 08-Polynomials & Factoring

A011 - Adding Polynomials
Go >
A012 - Subtracting Polynomials
Go >
A013 - Multiplying a Polynomial by Monomial (Distributing)
Go >
A014 - Dividing a Polynomial by a Monomial
Go >
A015 - Factor-Out the Greatest Common Factor
Go >
A117-Factoring GCF
Go >
A118-Multiplying Binomials
Go >
A119- Multiplying a Trinomial by a Binomial
Go >
A061-Binomial Times a Trinomial
Go >
A120- Multiplying Binomials (Special Cases)
Go >
A033 - Factoring Quadratics
Go >
A034 - Factoring Quadratics II
Go >
A035 - Difference of Two Perfect Squares
Go >
A121 - Factoring by Grouping
Go >

Algebra 1: 09-Quadratic Functions and Equations

A041 - Evaluate Quadratic Functions
Go >
A042 - Properties of Quadratic Equations
Go >
A122 - Solving Quadratic Equations By Taking Square Roots
Go >
A127 - Simplifying Rational Expressions
Go >
A057 - Completing the Square
Go >
A058 - Solve Equations by Completing the Square
Go >
A124- Completing the Square
Go >
A049 - Solve a System of Equations Graphically (Linear and Quadratic)
Go >
A052 - Solving a System of Equations Using Substitution
Go >

Algebra 1: 10-Radical Expressions & Functions

A045 - Pythagorean Theorem
Go >
A009 - Simplifying Radical Expressions
Go >
A063- Adding and Subtracting Radical Expressions
Go >
A064- Multiplying Radical Expressions
Go >
A065 - Dividing Radical Expressions
Go >
A060 - Solving Equations That Have Radical Terms
Go >
A125- Solving Radical Equations
Go >
A126- Graphing Square Root Functions
Go >
A046 - SOHCAHTOA
Go >
A047-Inverse Trigonometric Functions
Go >

Protected: Order – March 16, 2020 @ 08:13 PM


Algebra 1: 11-Rational Expressions & Functions

A127 - Simplifying Rational Expressions
Go >
A128-Multiplying and Dividing Rational Expressions
Go >
A129- Dividing Polynomials
Go >
A130- Adding & Subtracting Rational Expressions
Go >
A019 - Fractional Equations
Go >
A131- Solving Rational Equations
Go >
A132-Inverse Variation
Go >
A133- Graphing Rational Functions
Go >

Algebra 1: 12-Data Analysis & Probability

A134- Organizing Data Using Matrices
Go >
A135- Frequency and Histograms
Go >
A136- Measures of Central Tendency and Dispersion
Go >
A137- Box and Whisker Plots
Go >
A138- Samples and Surveys
Go >
A139- Permutations and Combinations
Go >
A140- Theoretical and Experimental Probability
Go >
A141 - Probability of Compound Events
Go >

I. Introduction to Algebra

Lesson: Verbal to Algebraic Expressions & Equations

Example: How do you write 5 greater than x algebraically?

Lesson: Declaring Variables

Example: Mike is 3 inches taller than Semande. If Semande is s inches tall, express Mike’s height in terms of s.

Lesson: Order of Operations

Example: Evaluate 3 - (5-8)^2

Lesson: Real Numbers (Including Rational vs. Irrational Numbers)

Lesson: Order of Operations with Substitution

Example: If x=2, what is the value of 2x^2-3x?

Lesson: Adding and Subtracting Real Numbers

Example: Evaluate 5 - (-2)

Lesson: Multiplying and Dividing Real Numbers

Example: Evaluate -3 \times 4

Lesson: Properties of Real Numbers

Example: Which property justifies the following equation: 5(x+2y)+5=5x+10y+5

Lesson: Distributive Property

Example: Simplify 3(4x-5)

Lesson: Finding the Solution to an Equation

Example: Is 7 a solution to the equation 12 = 3x - 9?

II. Solving Equations

Lesson: Solving Algebraic Equations (One-Step)

Example: Solve for x.
x+7=12

Lesson: Solving Multi-Step Equations

Example: Solve for x.
2x + 4 = 18

Lesson: Multi-Step Equations (Variable on Both Sides)

Example: Solve for x.
2x - 4 = -3x + 11

Lesson: Linear Equations

Example: Solve for y.
3y + 2x = 12

Lesson: Solving Proportions

Example: Solve for x.
\dfrac{x}{6} = \dfrac{20}{15}

Lesson: Solving Complex Proportions

Example: Solve for x.
\dfrac{x+5}{4} = \dfrac{3}{8}

Lesson: Percents

Example: What is 48% of 30?

Lesson: Percent Change

Example: What is the percent change from 50 to 72?

III. Solving Inequalities

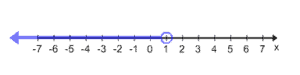
Lesson: Graphing Inequalities

Example: Graph k < 1
Algebra 1 Lessons

Lesson: Solving Inequalities Using Addition or Subtraction

Example: Solve for x.
x - 12 > 8

Lesson: Solving Inequalities Using Multiplication or Division

Example: Solve for x.
-4x \geq 12

Lesson: Solving Inequalities

Example: Solve for x.
-7x + 19 \leq -2

Lesson: Solving Compound Inequalities

Example: Solve for x.
-3 \leq 2x -5 < 21

Lesson: Solving and Graphing Compound Inequalities

Example: Solve for x and graph.
0 \leq r + 5 < 9
Algebra 1 Lessons

Lesson: Absolute Value Equations

Example: Solve for p.
9 + |5p + 1| = 18

Lesson: Absolute Value Inequalities

Example: Solve for x.
3|5x + 1| > 12

IV. Functions

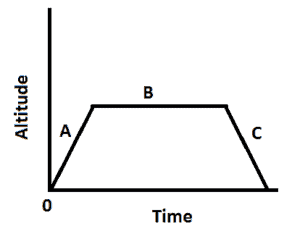
Lesson: Using Graphs to Relate Two Quantities

Example: A bird flies above ground in search of worms. This is represented in the table below.
Algebra 1 Lessons
What does A represent?

Lesson: Patterns and Linear Functions

Example: Is the following graph linear?
Algebra 1 Lessons

Example: For each set of ordered pairs, write the rule that represents the function.
(0, 3), (1, 8), (2, 13), (3, 18), (4, 23)

Lesson: Patterns and Non-Linear Functions

Example: Is the following a linear or nonlinear function?
Algebra 1 Lessons

Example: For the set of ordered pairs, write the rule that represents the function.
(0,1),(1,3),(2,9),(3,27),(4,81)

Lesson: Graphing a Function Rule

Example: Match the function with its graph.
Algebra 1 Lessons

Lesson: Writing a Function Rule

Example: Write the function rule for the table of values.
Algebra 1 Lessons

Lesson: Formalizing Relations and Functions

Example: Is the following relation shown a function?
(-2, 0.5), (0, 2.5), (4, 6.5), (5, 2.5)

V. Linear Functions

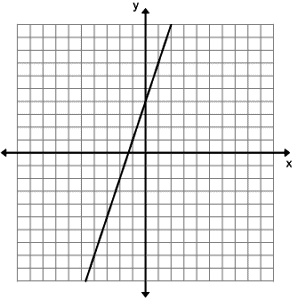
Lesson: Slope

Example: What is the slope of the line below?
Algebra 1 Lessons
Example: What is the slope of the line that passes through the points (2, 7) and (5, 12)?

Lesson: Equation of a Line

Example:

Lesson: Point Slope Form

Example:

Lesson: Finding the Equation of a Line, Given the Slope and a Point

Example:

Lesson: Standard Form of the Equations of a Line

Example:

Lesson: Finding the Equation of a Line, Given Two Points

Example:

Lesson: Equations of Parallel and Perpendicular Lines

Example:

Example:

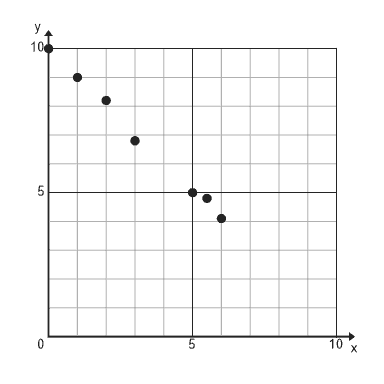
Lesson: Scatterplots and Trendlines

Example:

Algebra 1 Lessons

Lesson: Graphing Absolute Value Functions

Example:

VI. Systems of Equations and Inequalities

Lesson: Solving a System of Equations Graphically

Example:

Lesson: Solving a System of Equations Graphically

Example:

Lesson: Solving a System of Equations Using Substitution

Example:

Lesson: Solving a System of Equations Using Substitution

Example:

Lesson: Solving a System of Equations Using Elimination

Example:

Lesson: Solving a System of Equations Using Elimination

Example:

Lesson: Applications of Linear Systems

Example:

Lesson: Word Problems – System of Equations

Example:

Lesson: Word Problems – System of Equations

Example:

Lesson: Graphing Linear Inequalities

Example:

Lesson: Graphing Linear Inequalities

Example:

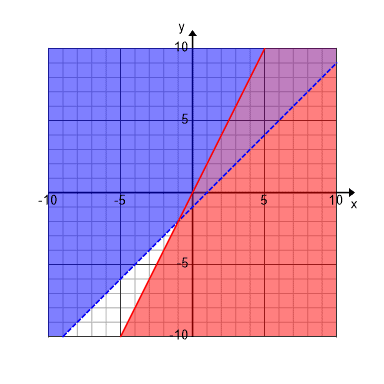
Algebra 1 Lessons

Lesson: Solving a System of Linear Inequalities

Example:

VII. Exponents and Exponential Functions

Lesson: Positive Exponents

Example:

Lesson: Negative Exponents

Example:

Lesson: Multiplying & Dividing Terms that have Exponents

Example:

Lesson: Multiplying & Dividing Terms that have Exponents

Example:

Lesson: Graphs of Exponential Functions

Example:

Lesson: Exponential Growth

Example:

Lesson: Exponential Decay

Example:

VIII. Polynomials and Factoring

Lesson: Adding & Subtracting Polynomials

Example:

Lesson: Adding & Subtracting Polynomials

Example:

Lesson: Multiplying a Polynomial by a Monomial

Example:

Lesson: Dividing a Polynomial by a Monomial

Example:

Lesson: Factor Out the Greatest Common Factor

Example:

Lesson: Factor Out the Greatest Common Factor

Example:

Lesson: Multiplying Binomials

Example:

Lesson: Multiplying a Binomial by a Trinomial

Example:

Lesson: Multiplying a Trinomial by a Binomial

Example:

Lesson: Multiplying Binomials (Special Cases)

Example:

Lesson: Factoring Quadratics

Example:

Lesson: Factoring Quadratics

Example:

Lesson: Difference of Perfect Squares

Example:

Lesson: Factoring by Grouping

Example:

IX. Quadratic Functions and Equations

Lesson: Evaluating Quadratic Functions

Example:

Lesson: Properties of Quadratic Functions

Example:

Lesson: Solving Quadratic Equations by Taking Square Roots

Example:

Lesson: Solving Equations by Factoring

Example:

Lesson: Completing the Square

Example:

Lesson: Solve Equations by Completing the Square

Example:

Lesson: Vertex Form of a Quadratic Function by Completing the Square

Example:

Lesson: Solving a System of Equations Graphically (Linear & Quadratic)

Example:

Lesson: Solving a System of Equations Using Substitution (Linear & Quadratic)

Example:

X. Radical Expressions and Functions

Lesson: Pythagorean Theorem

Example:

Lesson: Simplifying Radical Expressions

Example:

Lesson: Adding and Subtracting Radical Expressions

Example:

Lesson: Multiplying Radical Expressions

Example:

Lesson: Dividing Radical Expressions

Example:

Lesson: Solving Equations That Have Radical Terms

Example:

Lesson: Solving Equations That Have Radical Terms

Example:

Lesson: Graphing Square Root Functions

Example:

Lesson: SOHCAHTOA (sine, cosine, tangent)

Example:

Lesson: Inverse Trigonometric Functions

Example:

XI. Rational Expressions and Functions

Lesson: Simplifying Rational Expressions

Example:

Lesson: Multiplying and Dividing Rational Expressions

Example:

Lesson: Dividing Polynomials

Example:

Lesson: Adding and Subtracting Rational Expressions

Example:

Lesson: Fractional Equations

Example:

Lesson: Solving Rational Equations

Example:

Lesson: Inverse Variation

Example:

Lesson: Graphing Rational Functions

Example:

XII. Data Analysis and Probability

Lesson: Matrices

Example:

Algebra 1 Lessons

Lesson: Frequency, Cumulative Frequency, & Histograms

Example:

Lesson: Measures of Central Tendency & Dispersion

Example:

Lesson: Box & Whisker Plot

Example:

Lesson: Samples and Surveys

Example:

Lesson: Permutations and Combinations

Example:

Lesson: Theoretical vs. Experimental Probability

Example:

Lesson: Probability of Compound Events

Example:

Sign up for a free membership on our algebra 1 lessons & start learning today. Learn about the importance of learning algebra here.