Equation Of A Line

Learn about the equation of a line. After you finish this lesson, view all of our Pre-Algebra lessons and practice problems.

Equation of a Line (Slope-Intercept Form)

y=mx+b

where m = slope and b = y-intercept.

To find the slope, use the slope formula:

m = \dfrac{y_2 - y_1}{x_2 - x_1}

Examples of Equation of a Line

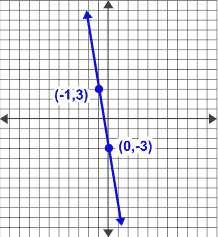
Example 1

First, let’s determine the coordinates of the points

P_1(-1,3) and P_2(0,-3)

Then, solve for the slope

m = \dfrac{y_2 - y_1}{x_2 - x_1} m = \dfrac{-3-3}{0-{-}1} m=-6

Slope-intercept form is y = mx + b

Where m = slope and b = y-intercept

Now, our y-interecept is -3

b = -3

Substitute the given and we have

y = -6x-3

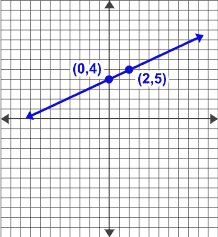
Example 2

First, let’s determine the coordinates of the points

P_1(0,4) and P_2(2,5)

Then, solve for the slope

m = \dfrac{y_2 - y_1}{x_2 - x_1} m = \dfrac{5-4}{2-0} m=\dfrac{1}{2}

Slope-intercept form is y = mx + b

Where m = slope and b = y-intercept

Now, our y-interecept is 4

b = 4

Substitute the given and we have

y = \dfrac{1}{2}x+4

Video-Lesson Transcript

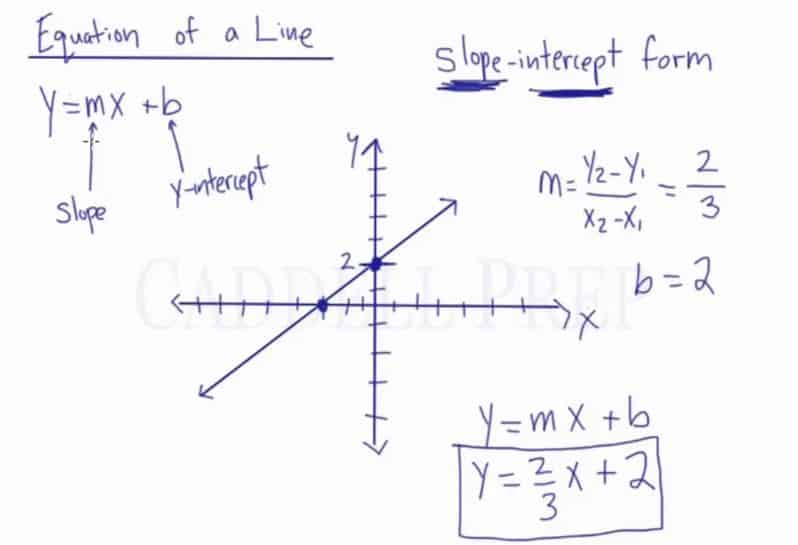
In this lesson, we’ll review the equation of a line and go over the slope-intercept form which is the most common equation of a line.

It’s called slope-intercept form for a very specific reason.

When we look at the equation, we will know what our slope is and its intercept.

Intercept is where a line segment intersects the axis. The y-intercept is the point where the line segment crosses or touches the y-axis.

Slope-intercept form is

y = mx + b

Where m = slope and b = y-intercept

Our formula for slope is

m = \dfrac{y_1 - y_2}{x_1 - x_2}

Let’s look at the graph.

Then count the change in y and x from the origin with (0, 0)coordinates.

So we have

m = \dfrac{2}{3}

Now, let’s refer back to the graph and look where the line intersects the y-axis. Meaning, find the point where the line meets the y– axis and where the x-axis is 0.

Now, our y-interecept is 2.

So now b = 2.

Now, we’re ready to write the slope-intercept form.

Substitute the given and we have

y = mx + b y = \dfrac{2}{3} x + 2

So our slope-interecept form is

y = \dfrac{2}{3} x + 2

Equation Of A Line

Again, the slope-intercept form is

y = mx + b

Where m = slope and b = y-intercept.