Learn Inverse Trigonometric Functions

In this lesson, we’re going to go over inverse trigonometric functions. After you finish this lesson, view all of our Algebra 1 lessons and practice problems.

The same SOHCAHTOA from the previous lesson will be needed to perform the functions.
$sin\theta = \dfrac{opposite}{hypotenuse}$
$cos\theta = \dfrac{adjacent}{hypotenuse}$
$tan\theta = \dfrac{opposite}{adjacent}$

For example:
$sin\theta = \dfrac{5}{10}$

Perform the inverse of sin in this situation.
$sin^{-1}(sin\theta) = sin^{-1}(\frac{5}{10})$

Enter $sin^{-1}$ into the calculator and insert the expression
$\theta = sin^{-1}(\dfrac{5}{10})$
$\theta = 30$

Example of Inverse Trigonometric Functions

Example 1

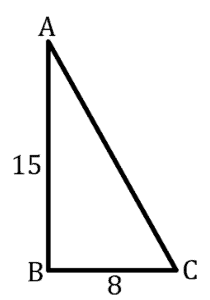
Given that $\triangle ABC$ is a right triangle with $\angle B$ as the right angle, $\overline{AB} = 15$ and $\overline{BC} = 8$ . What is the measure of $\angle A$ ?

We have an angle, the opposite side= $8$ , and the adjacent side= $15$ .

$\tan \theta = \dfrac{opposite side}{adjacent side}$
$\tan \theta = \dfrac{8}{15}$
$\theta = \tan^{-1} (\dfrac{8}{15})$
$\theta = 28^\circ$

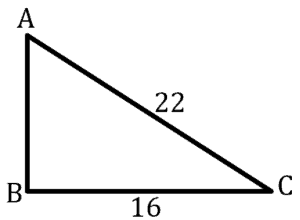
Example 2

Given that $\triangle ABC$ is a right triangle with $\angle B$ as the right angle, $\overline{AC} = 22$ and $\overline{BC} = 16$ . What is the measure of $\angle C$ ?

We have an angle, the adjacent side= $16$ , and the hypotenuse= $22$ .

$\cos \theta = \dfrac{adjacent side}{hypotenuse}$
$\cos \theta = \dfrac{16}{22}$
$\theta = cos^{-1} (\dfrac{16}{22})$
$\theta =43\circ$

Video-Lesson Transcript

In this lesson, we’re going to go over inverse trigonometric functions.

If you remember from sine, cosine, and tangent, we use those to find missing sides when we have an angle and one side.

We use inverse trigonometric functions to find the angle.

Let’s draw a right triangle and we are given two sides. And we have to find the angle theta.

First, let’s choose which trigonometric function to use.

So we have

SOH CAH TOA

Here we have an angle, the opposite side, and the hypotenuse.

$\sin \theta = \dfrac{opposite side}{hypotenuse}$

$\sin \theta = \dfrac{x}{y}$

The given values are

$x = 5$ which is the opposite side
$y = 10$ which is the hypotenuse

Then, we’ll have

$\sin \theta = \dfrac{5}{10}$

and we need to find what theta is.

Some students confused the solution to divide by sine.

But that’s not the case. Because it’s not sine times theta. It is the sine of theta.

So, what we need to do is the inverse of sine.

Let’s do the inverse of sine on both sides.

$\sin^{-1} (\sin \theta) = \sin^{-1} (\dfrac{5}{10})$

$\theta = \sin^{-1} (\dfrac{5}{10})$

Please note that $\arcsin = \sin^{-1}$ . They have the same meaning.

Going back, if you have it on your calculator you’ll find out that

$\theta = 30$

Again, if we’re looking for the angle, we eventually should do the inverse of sine, cosine, and tangent.

But we can start by setting it up with our regular formula.

And this is true in any combination. Not only in sine.

For example, we don’t have the value of the opposite side.

But we have the adjacent side, which is

$5 \sqrt{3}$

and we’re still looking for the angle theta.

So, we should use the formula for cosine.

$\cos \theta = \dfrac{adjacent side}{hypotenuse}$

$\cos \theta = \dfrac{5 \sqrt{3}}{10}$

Again, we have to do the inverse of cosine.

$\theta = cos^{-1} (\dfrac{5 \sqrt{3}}{10})$

Using the calculator, our answer is

$\theta = 30^{\circ}$

Now, let’s see one more example. We’ll usse the inverse of tangent.

Here, the hypotenuse isn’t given.

But we have the opposite side $= 5$ and the same value for the adjacent.

So, let’s use the formula for tangent.

$\tan \theta = \dfrac{opposite side}{adjacent side}$

$\tan \theta = \dfrac{5}{5 \sqrt{3}}$

Now, to get the theta, we’ll use the inverse of tangent on both sides.

$\theta = \tan^{-1} (\dfrac{5}{5 \sqrt{3}})$

$\theta = 30^{\circ}$

Again, if we have two sides and we’re missing the angle, we can easily just set up our sine, cosine, and tangent functions like normal.

Then to solve for theta, we’ll do the inverse of that trigonometric function.