Learn SOHCAHTOA (Sine, Cosine, And Tangent)

Learn how to apply sine, cosine, and tangent (SOHCAHTOA) in right triangles to solve for missing lengths or angles in a right triangle. After you finish this lesson, view all of our Algebra 1 lessons and practice problems.

What is SOHCAHTOA?

SOH CAH TOA

SOH stands for Sine, Opposite, Hypotenuse and gives us $sin\theta = \dfrac{opposite}{hypotenuse}$

CAH stands for Cosine, Adjacent, Hypotenuse and gives us $cos\theta = \dfrac{adjacent}{hypotenuse}$

TOA stands for Tangent, Opposite, Adjacent and gives us $tan\theta = \dfrac{opposite}{adjacent}$

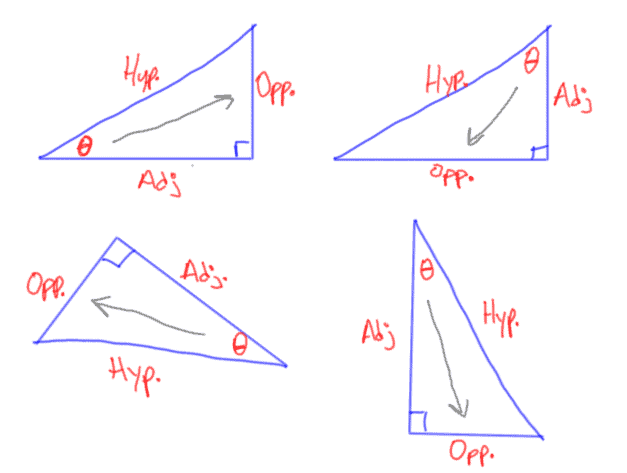
What are the opposite, adjacent and hypotenuse in a right triangle?

Hypotenuse – the hypotenuse of a right triangle is the longest side in a right triangle; it is also always across from the right angle
Opposite side – the opposite side is the side across from (opposite of) the selected angle
Adjacent side – the adjacent side is the side next to the selected angle; it’s the side that isn’t the hypotenuse or the opposite side

Note: The opposite side and adjacent side are always in reference to an angle.

Above are four examples of identifying the hypotenuse, adjacent side and opposite side in right triangles. The opposite side is found by looking across from the indicated angle.

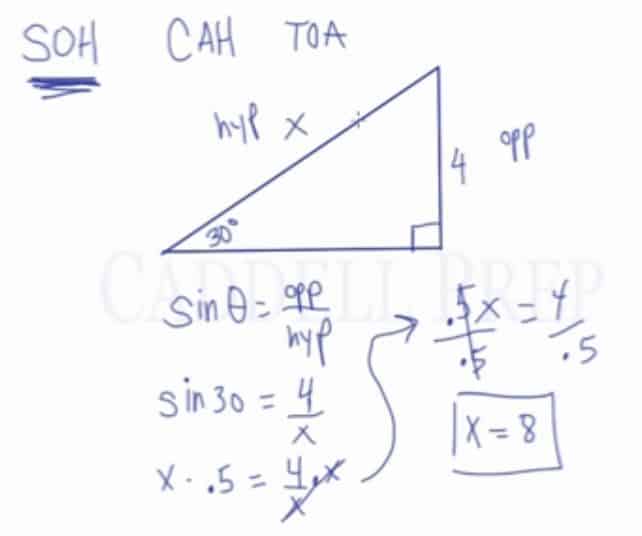
Here is an example of how to use SOHCAHTOA:

In a right triangle, one leg has a measure of 4 units and the opposite angle has a measure of 30 degrees. Determine the length of the hypotenuse.

Since the angle measure given is opposite of the side and the question asks to find the hypotenuse, sin can be used to find the missing length.
$sin\theta = \frac{opposite}{hypotenuse}$

Substitute the variables
$sin 30= \frac{4}{hypotenuse}$

Solve for sin 30
$0.5 = \frac{4}{x}$

Multiple x on both sides
$0.5x = \frac{4}{x}\times x$
$0.5x = 4$

Divide 0.5 on both sides to isolate x
$x = 8$
The hypotenuse is 8 units

Examples of SOHCAHTOA (sine, cosine, tangent)

Example 1

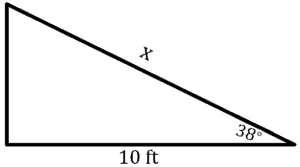
A ramp is pulled out of the back of the truck. There is a $38$ degrees angle between the ramp and the pavement. If the distance from the end of the ramp to the back of the truck is $10$ feet. How long is the ramp?

First, let’s draw a diagram and assign the given values

The given is the angle and adjacent side. So, we are going to solve its hypotenuse
Now, let’s solve using Cosine
$\cos \theta = \dfrac{adjacent side}{hypotenuse}$

$\cos (38) = \dfrac{10}{x}$ $x= \dfrac{10}{\cos (38) }$ $x=12.69$

Therefore, the answer is $12.69$ feet

Example 2

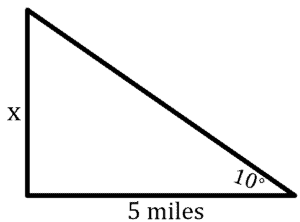
A man sees a rocket at an angle of elevation of $11$ degrees. If the man is located at $5$ miles from the rocket launch pad, how high is the rocket? Round the answer to the nearest hundredth.

First, let’s draw a diagram and assign the given values

The given is the angle and adjacent side. We are looking for the rocket’s height
Now, let’s solve using Tangent

$\tan \theta = \dfrac{opposite side}{adjacent side}$ $\tan (10) = \dfrac{x}{5}$ $\tan(10)(5)=x$ $0.88=x$

Therefore, the answer is $0.88$ miles

Video-Lesson Transcript

In this lesson, we’ll go over basic trigonometry.

So, we’re going to review sine, cosine, and tangent.

A sine of an angle, a cosine of an angle, and a tangent of an angle represent ratios of sides of a right triangle.

If we’re given an angle of one side, we can use one of these trigonometric functions to find the other sides.

For example:

$\sin \theta = \dfrac{opposite side}{hypotenuse}$

I’ll review what side is the opposite and the hypotenuse later.

$\cos \theta = \dfrac{adjacent side}{hypotenuse}$ $\tan \theta = \dfrac{opposite side}{adjacent side}$

One way to memorize this is memorize:

SOH CAH TOA

S – sine
O – opposite
H – hypotenuse

C – cos
A – adjacent
H – hypotenuse

T – tangent
O – opposite
A – adjacent

Let’s draw a right triangle.

Then let’s define the sides.

The side across from the right angle is the hypotenuse.

Next, the opposite of theta is called the opposite side.

And lastly, the side next to theta is called the adjacent side.

Let’s look at this example:

We have a right triangle. One angle is $30^{\circ}$ angle. One side is $4$ . And we’re searching for the hypotenuse.

If we have one side, we can easily use the Pythagorean theorem. But since we are missing the measurement of this side, so we can’t.

Instead, we have to use one of these trigonometric relationships to figure out what the hypotenuse is.

A good place to start is to write our abbreviation.

SOH CAH TOA

So we can determine which one we’re going to use.

Now, let’s figure out what sides we have.

$4$ is across the angle, so that’s the opposite side.

$x$ , which we’re looking for, is right across the right angle. That’s the hypotenuse.

So, we’re going to use SOH.

Since sine has opposite and hypotenuse in it.

$\sin \theta = \dfrac{opposite side}{hypotenuse}$

$\sin 30 = \dfrac{4}{x}$

Now, $\sin 30 = 0.5$ which you can find out using a calculator or you can memorize that $\sin 30$ is $\dfrac{1}{2}$ .

$0.5 = \dfrac{4}{x}$

$0.5 \times x = \dfrac{4}{x} \times x$

$0.5x = 4$

$\dfrac{0.5x}{0.5} = \dfrac{4}{0.5}$

$x = 8$

This should make sense because $\sin 30 = 0.5$ . That means opposite of hypotenuse is $0.5$ .

$\dfrac{4}{8}$ is $0.5$

It does make sense at the end.

So in solving for one of the missing sides and we are given an angle and one side, we can usually find the other side by using sine, cosine, or tangent.

First, we just have to identify what sides were given.

And then write the formula and solve.