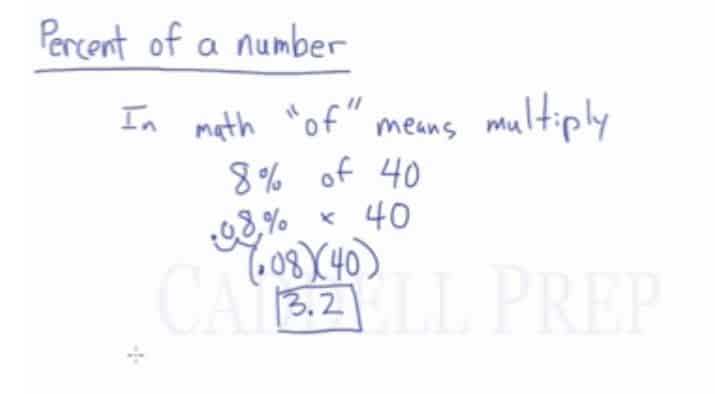In this video, we will be learning how to find a percent of a number using proportions. After you finish this lesson, view all of our Pre-Algebra and Algebra lessons and practice problems.
In math, “of” means multiply
Percent Formula:
Example of Finding the Percent of a Number
What is 8% of 40?
First we cross-multiply
Then we divide by 100 on both sides to isolate x
Example 1
What is of
?
First, we cross-multiply
Then, we divide by on both sides to isolate
The answer is
Example 2
What percent of is
?
We have the “of” and the “is”. Our formula should look like this:
Let’s cross multiply
is
is
We have:
Now, let’s divide both sides by
Therefore, the answer is
Video-Lesson Transcript
In this video, we will be learning how to find a percent of a number using proportions.
In math, ‘of’ means ‘multiply‘.
So if you’re asked of
, it means
.
We can’t get the answer right away.
We have to change into a decimal.
So we have to move the decimal two spaces from the right to left.
will become
then we can multiply
Another way to find the percent of a number is the percent formula.
Percent formula is
Let’s answer this question:
What is of
?
Let’s use the formula
Let’s cross-multiply
is
is
Now we have
To isolate , let’s do the inverse operation.
We just have to divide both sides by
And we get
Which is the same answer using a different method.
To sum up, you can multiply or use the percent formula to get the answer if the missing value is the “is” or the part.
But if the missing value is the percent or the whole, you have to use the percent formula.
To give an example, let’s answer this question:
What percent of is
?
Here, we’re looking for the percent. We have the “of” and the “is”.
The formula is
Since we’re missing the percent, our formula should look like this
Then let’s cross multiply
is
is
Now, let’s do the inverse operation of multiplication which is division.
So, let’s divide both sides by
The answer is
So the answer to what percent of is
?
The answer is