Solving Algebraic Equations (One-Step)

In this video, students will be learning how to solve algebraic equations using inverse operations. After you finish this lesson, view all of our Pre-Algebra and Algebra 1 lessons and practice problems.

For example:

36 = 9x

To solve for x, we will use inverse operations.

Since x is being multiplied by 9, the inverse operation would be to divide both sides by 9.

\frac{36}{9}=\frac{9x}{9} \leftarrow Divide by 9 on both sides

4 = x

Examples of Solving Algebraic Equations (One-Step)

Examples 1

x+5=30

We have to eliminate 5 by subtracting 5 on both sides

Therefore,

x+5-5=30-5

Now, we have:

x=25

Examples 2

8x=56

To solve for x, we will use inverse operations.

Since x is being multiplied by 8, the inverse operation would be to divide both sides by 8

\dfrac{8x}{x}=\dfrac{56}{8}

Now, we have:

x=7

Video-Lesson Transcript

In this video, students will be learning how to solve algebraic equations using inverse operations.

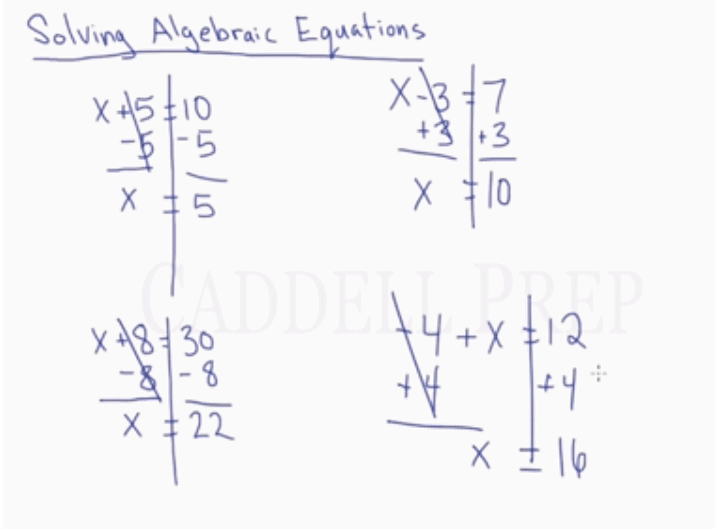
Solving Equations that Have Addition or Subtraction

Let’s start off with some simple ones.

x + 5 = 10

To get the value of x we have to subtract 5 from both sides of the equation.

It may be useful to draw a long vertical line through the equal sign. For you to remember that whatever you do on one side, you have to do on the other side, too.

The answer is x = 5.

Let’s have more examples.

x + 8 = 30

We have to subtract 8 from both sides.

And we will come up with x = 22.

Here, we have x - 3 = 7.

To get rid of - 3 we have to add 3 on both sides.

Now we have x = 10.

Also, let’s do {-4} + x = 12.

To get rid of {-4} we should add 4.

So we’ll have x = 16.

Solving Algebraic Equations One-Step

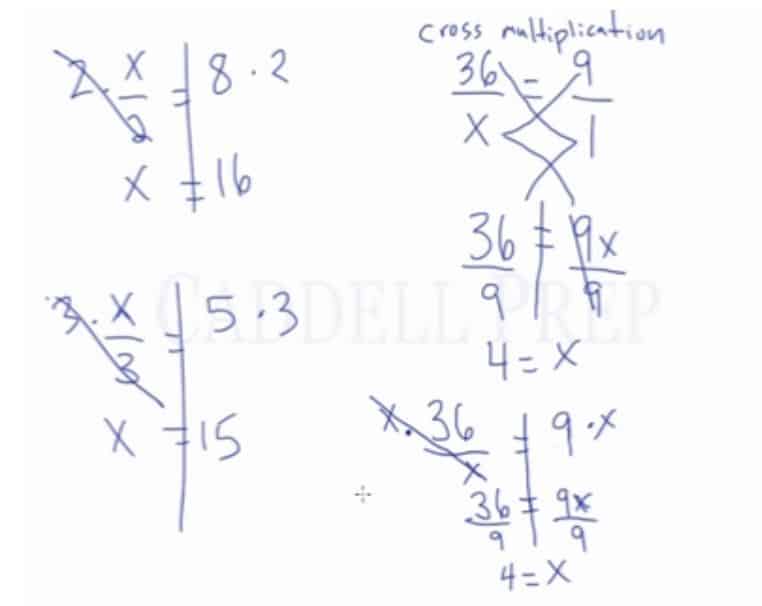
Solving Equations that Have Multiplication or Division

Let’s now look at some examples involving multiplication.

So for example, we have 3x = 12. This means 3 \times x = 12.

To do this, we have to identify that the inverse of multiplication is division.

So we have to divide both sides by 3.

We will come up with x = 4.

More example: 2x = 30

Then divide both sides by 2

The answer is x = 15

Let’s have 5x = 25 then divide both sides by 5 to get x = 5.

Another example is {-3x} = 18.

Don’t be tricked by the negative sign. It is not a subtraction sign.

So to get rid of {-3} we just have to divide both sides by {-3}.

And the answer is x = {-6}

Solving Algebraic Equations

Now, let’s have examples involving division.

\dfrac{x}{2} = 8

So we have to do the inverse of division which is multiplication. Let’s multiply both sides by 2.

And we get x = 16.

Let’s also try \dfrac{x}{3} = 5. Then multiply both sides by 3. We’ll have x = 15.

Here’s another method to solve equations involving division. You may have seen it before. It is called ‘cross-multiplication’.

We have \dfrac{36}{x} = 9

To do cross-multiplication, it’s important to show both sides of the equation as fractions. So we should have \dfrac{36}{x} = \dfrac{9}{1}.

What we’re going to do is 36 \times 1 = 36.

Then 9 \times x = 9x.

We have 36 = 9x.

We still want to isolate x so we’ll divide both sides by 9.

The answer is 4 = x.

Solving Equations that Involve Cross-Multiplication

Now let’s solve it without cross-multiplication.

\dfrac{36}{x} = 9

Let’s multiply both sides by x and we have 36 = 9x.

This is similar to the one above.

So let’s divide both sides by 9 and we still find that 4 = x.

Solving Algebraic Equations 2

To sum up, for simple algebraic equations, we just can do inverse operations to get the value of x.