Add & Subtract Polynomials

In this video, learn how to add & subtract polynomials by combining like terms. After you finish this lesson, view all of our Pre-Algebra lessons and practice problems.

In this video, we are going to look at adding and subtracting polynomials.
For example:
To simplify the expression:

combine the like terms to get the final answer of

To simplify the expression:

we can either keep-change-change or distribute the negative to get

Then, combine like terms to get the final answer of

Sometimes, every term may not line up, such as in the expression

Solve as you would normally by either keep-change-change or distributing the negative, and then combining like terms to get a final answer of

Examples of Adding and Subtracting Polynomials

Example 1

Combine the like terms

Now, we have

Example 2

First, distribute the negative sign to the terms inside the second parenthesis

Then, combine the like terms

Now, we have

Video-Lesson Transcript

Now, let’s discuss how to add and subtract polynomials.

For example, we have

It’s helpful to align the like terms so its easier to combine them.

Now, we combine the like terms

Or we can write the two polynomials on a straight line like this:

Now, we distribute the sign.

It’s like we have at the beginning of the polynomial inside the parenthesis.

So we’ll have

Then, look for the like terms and combine them.

We got the same answer as the first.

Let’s look at an example which involves subtraction.

Since we’re subtracting polynomials, we should do keep-change-change.

Let’s keep the top the same.

Then change the overall minus sign into addition.

Lastly, we change the signs of each term.

Now, it’s time for us to combine the like terms

And the answer is

Now, let’s do this on a straight line.

Let’s distribute the negative sign into the polynomial in the parenthesis. Just like there’s a at the beginning.

So, we’ll have

Then, combine the like terms. We now have

Same as the first answer.

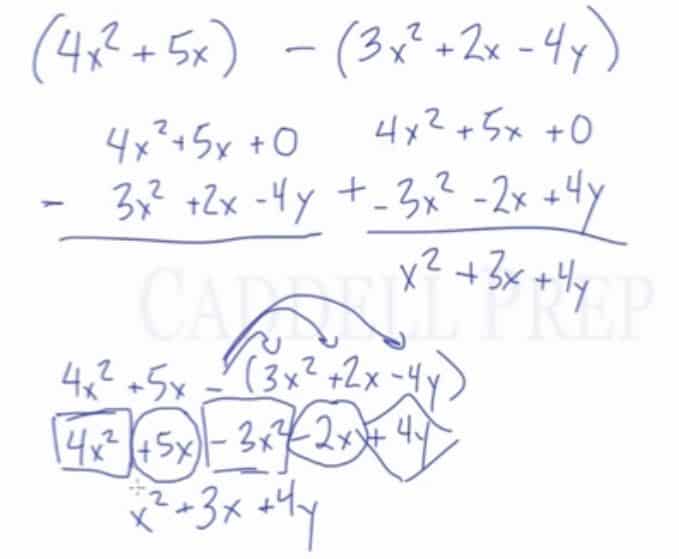
Let’s look at a pretty difficult problem here

Let’s solve this using the two-row format.

Since there’s nothing above the , we can put in as a place holder.

Then, let’s do keep-change-change since we have subtraction.

It will look like this now

After combining the like terms, the answer is

Now, let’s solve in a horizontal line format

Let’s distribute the negative sign into the polynomial in the parenthesis.

Then, combine like terms.

And we got the same answer.