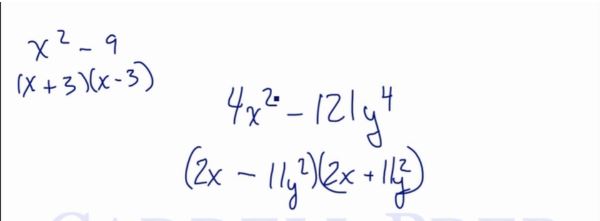In this video, we are going to look at how to understand the difference of perfect squares. After you finish this lesson, view all of our Algebra 1 lessons and practice problems.
For example:
When given something like , we can rewrite it as
To factor this, we will need two numbers that add up to 0 and multiply to -9. These numbers are 3 and -3. Therefore when we factor this, we will get
Generally, whenever we have we will always be able to factor it as
Or
will always be factored as
For expressions more complex, such as
First, take the square root of the first term and place it in the front of each set of parentheses, and then take the square root of the second term and place it in the two parentheses with a plus or minus sign. This will be factored as
Example of Difference Of Perfect Squares
Example 1
Factor
will always be factored as
Therefore, this will be factored as
Factor
First, take the square root of the first term and place it in front of each set of parentheses.
Then take the square root of the second term and place it in the two parentheses with a plus or minus sign.
Therefore, this will be factored as
Video-Lesson Transcript
Let’s go over the difference of perfect squares.
Let’s have some examples.
The difference is associated with subtraction. That’s why we have a subtraction sign here.
Perfect squares are numbers that are the square root of.
The difference of perfect squares means two perfect squares to be subtracted.
Let’s take a look at how to factor these.
Next,
And
In general, the form is:
So if we have a perfect square
So if we have
And of course, this can be switched into
It doesn’t make any difference.
This rule applies to all perfect squares.
For example:
Let’s find the square root of the first term then the square root of the second term.
So our answer is
Look at this previous example:
Let’s draw two parenthesis and put an inside each parenthesis.
If you solve that, the square root of is
.
Then the squareroot of is
.
So our answer is
So for , we’ll find the squareroot of each term.
The squareroot of is
. The squareroot of
is
. Then the squareroot of
is
. Lastly, the squareroot of
is
.