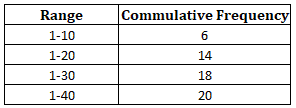Frequency, Cumulative Frequency, & Histograms

Frequency and Cumulative Frequency

In the first video, we are going to use frequency and cumulative frequency. After you finish this lesson, view all of our Algebra 1 lessons and practice problems.

For example:
List: 3, 3, 3, 9, 12, 14, 14, 15, 19, 29, 34, 34, 35, 36, 37

Let’s make a table to group the numbers. Make sure that the intervals are the same for all groups.

Frequency

Range Tally Frequency
0<n\leq5 ||| 3
5<n\leq10 | 1
10<n\leq15 |||| 4
15<n\leq20 | 1
20<n\leq25 0 0
25<n\leq30 | 1
30<n\leq35 ||| 3
35<n\leq40 || 2

Cumulative frequency starts from the first value, and the initial value remains when moving on to the next group.

For example:

Range Tally Frequency
0<n\leq5 ||| 3
0<n\leq10 |||| 4
0<n\leq15 |||| ||| 8
0<n\leq20 |||| |||| 9
0<n\leq25 |||| |||| 9
0<n\leq30 |||| |||| 10
0<n\leq35 |||| |||| ||| 13
0<n\leq40 |||| |||| |||| 15

Examples of Frequency, Cumulative Frequency, & Histograms

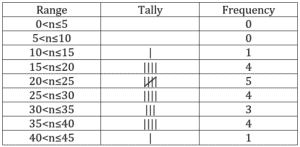
Example 1

List: 15, 18, 19, 20, 20, 22, 22, 22, 24, 25, 26, 27, 28, 28, 34, 34, 35, 38, 39, 40, 40, 45
Frequency

Cumulative Frequency

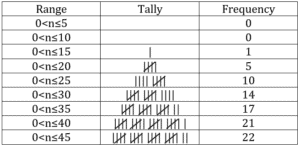
Example 2

List: 1, 1, 1, 3, 4, 4, 5, 6, 6, 8, 8, 8, 8, 9, 9, 9, 10, 11, 12, 12, 15, 15, 18, 18, 18, 19, 20, 22, 22, 25, 25, 25, 28, 29, 29
Frequency

Cumulative Frequency

Video-Lesson Transcript

Let’s go over frequency and cumulative frequency.

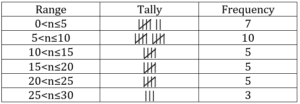
Let’s start with this:

3, 3, 3, 9, 12, 14, 14, 15, 19, 28, 34, 34, 35, 36, 37

Let’s draw a table and label them with range, tally, and frequency.

Ranges are:

0 \textless n \leq 5
5 \textless n \leq 10
10 \textless n \leq 15
15 \textless n \leq 20
20 \textless n \leq 25
25 \textless n \leq 30
30 \textless n \leq 35
35 \textless n \leq 40

A couple of things to note:

1. Because I’m using less than or equal to sign, I can’t repeat values here. The next range should be bigger than the previous range.

2. Size of each range is exactly the same.

Now, we’re ready to tally the numbers using the ranges.

0 \textless n \leq 5 has |||
5 \textless n \leq 10 has |
10 \textless n \leq 15 has ||||
15 \textless n \leq 20 has |
20 \textless n \leq 25 has 0
25 \textless n \leq 30 has |
30 \textless n \leq 35 has |||
35 \textless n \leq 40 has ||

Then let’s write the actual frequency.

0 \textless n \leq 5 has ||| is 3
5 \textless n \leq 10 has | is 1
10 \textless n \leq 15 has |||| is 4
15 \textless n \leq 20 has | is 1
20 \textless n \leq 25 has 0 is 0
25 \textless n \leq 30 has | is 1
30 \textless n \leq 35 has ||| is 3
35 \textless n \leq 40 has || is 2

So, this is our frequency chart.

Same thing with a cumulative chart.

Let’s label the table with range, tally, and cumulative frequency.

Ranges are:

0 \textless n \leq 5
0 \textless n \leq 10
0 \textless n \leq 15
0 \textless n \leq 20
0 \textless n \leq 25
0 \textless n \leq 30
0 \textless n \leq 35
0 \textless n \leq 40

Instead of starting with the highest number for the next range, we’re still going to start with 0 for all the ranges.

Now, let’s tally.

0 \textless n \leq 5 has |||
0 \textless n \leq 10 has ||||

0 \textless n \leq 15 has |||| |||

0 \textless n \leq 20 has |||| ||||

0 \textless n \leq 25 has |||| ||||

0 \textless n \leq 30 has |||| ||||

0 \textless n \leq 35 has |||| |||| |||

0 \textless n \leq 40 has |||| |||| ||||

Now, let’s write the cumulative frequency.

0 \textless n \leq 5 has ||| is 3
0 \textless n \leq 10 has |||| is 4
0 \textless n \leq 15 has |||| ||| is 8
0 \textless n \leq 20 has |||| |||| is 9
0 \textless n \leq 25 has |||| |||| is 9
0 \textless n \leq 30 has |||| |||| is 10
0 \textless n \leq 35 has |||| |||| ||| is 13
0 \textless n \leq 40 has |||| |||| |||| is 15

You should notice that as you move down the table, cumulative frequency increases or remains the same. But definitely does not go down.

Each next row can have the previous number or increase it. But definitely not be less than the previous range.

Now, let’s take a look at this.

We can actually get the cumulative frequency by using the first table.

Let’s make sense of this.

From 0 to 5, we included three in the group.

Then in 0 to 10, we expanded and included one more. So from 3 to 4.

Then in 0 to 15, we already have 4 and included four more numbers. The cumulative frequency increased by 4. So now, we have 8.

Then when we move up to 20, we added one more.

When we move up to 25, none added. So, we stayed at 9.

Up to 30, we included one more. So the group became 10.

When we move to 35, we added three more. So our cumulative frequency is 13.

Lastly, moving up to 40, we included two more numbers. Now, we have 15.

Let’s see how we get that from this table.

We just have to add the next frequency to the previous, we’ll get the cumulative frequency.

Representing Frequency and Cumulative Frequency with a Histogram

In the second video, we are going to create a histogram.

Examples of Representing Frequency and Cumulative Frequency with a Histogram

Example 1

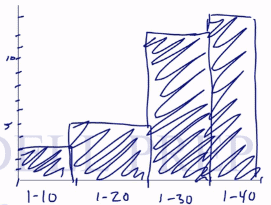
Representing Frequency with Histogram

Example 2

Representing Cumulative Frequency with Histogram

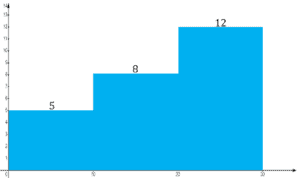
Histogram:
Let’s use the same list from the first video. Histograms look relatively close to bar graphs with minor changes, but the overall ideas are the same. Mark the x-axis with the desired intervals and the y-axis with the values. Make sure that the values are increasing at a constant rate.

histogram frequency

For the cumulative frequency, each interval of the histogram is going to be the sum from the first interval to the current interval as shown below:

histogram cumulative frequency

Video-Lesson Transcript

Let’s go over histograms frequency and cumulative frequency.

For example:

Range is 1 - 10 the frequency is 3.

In range 11 - 20 the frequency is 2.

In range 21 - 30 the frequency is 7.

In range 31 - 40 the frequency is 1.

Now, let’s graph this.

The x-axis represents the range while the y-axis represents the frequency.

Then let’s draw a bar.

This looks like a bar graph but the most important thing is that they are touching each other.

There are no spaces in between. Unless the frequency of a range is zero.

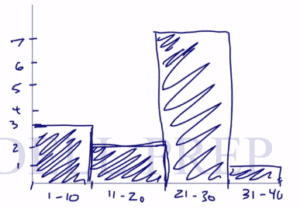
Now, let’s graph the cumulative frequency using the same information as above.

Range is 1 - 10 the frequency is 3.

In range 1 - 20, we included two more so the frequency is 5.

We’ll jump to 30, we’ll pick up seven more values. So, the frequency is 12.

Then we’ll jump up to 40, we have to add one more. With a total frequency of 13.

Now, we’re ready to graph.

We’ll just change the values on the y-axis to match our frequency.

The intervals stay the same.

Once you draw a bar graph, shade it in.

Cumulative frequency increases so the bar increases also.

Or they can be of the same height. But never decrease.

Using this histogram, we can see the group in the range 31 - 40.

Range 1 - 40 is 13.
Range 1 - 30 is 12.

So, what’s the difference?

One. That’s the frequency in 31 - 40.

Likewise, we want to see how many are in the interval from 21 - 30.

Let’s look at how many are there up to 30 inclusive there are 12. But up to 20, we only have 5.

So how many were added when we included up to 30?

Seven. So from 21 - 30, there are 7 in the group.

In the frequency table, we also have 7.

To find 11 - 20, 1 - 20 has 5 values and 1 - 10 has 3 values. So, there’s 2 in 11 - 20.

Which is the same as the table.