Learn About Properties Of Quadratic Functions

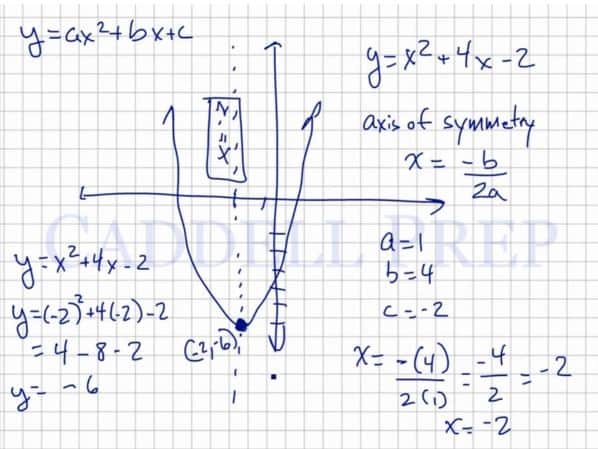
In this video, we are going to look at properties of quadratic functions. Quadratic functions are written in the form $y=ax^2+bx+c$ . The most basic one is $y=x^2$ . These functions are parabolas and are “U”-shaped. The point where it stops and changes to the other direction is known as the vertex. The axis of symmetry of the parabola passes through the vertex. After you finish this lesson, view all of our Algebra 1 lessons and practice problems.

A graphing calculator is a helpful tool when it comes to dealing with quadratic functions. After graphing the function, the vertex can sometimes be seen as a point on the table. The axis of symmetry has the equation of the x-coordinate of the vertex. In the function $y=x^2+4x-2$ the table helped us determine that the vertex lies at (-2,-6).
Without a graphing calculator, we can still find this information.
The formula for the axis of symmetry is written as $x=\dfrac{-b}{2a}$
In the function $y=x^2+4x-2$ $a=1, b=4, c=-2$ . When these values are substituted into the formula, $x=\dfrac{-(4)}{2(1)}$ we find that the axis of symmetry is at x=-2.
Since the vertex is a point on the graph, we can use the original function and the x-value of the axis of symmetry to solve for the point where the vertex lies.
If we substitute -2 for x in this function, we have
$y=(-2)^2+4(-2)-2$
which is simplified to
$y=4-8-2$
and finally
$y=-6$
This means that the vertex lies at the point (-2,-6), which agrees with the same point that we determined from the graphing calculator.

Examples of Properties of Quadratic Functions

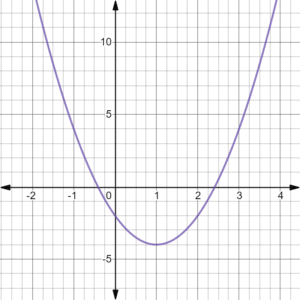
Example 1

$y = x^2+ 16x + 64$
The axis of symmetry is $x = \dfrac{-b}{2a}$
our values are as follows:
$a = 1$
$b = 16$
$c = 64$

Now, let’s solve for the axis of symmetry

$x = \dfrac{-b}{2a}$
$x = \dfrac{-16}{2(1)}$
$x = \dfrac{-16}{2}$
Final answer is
$x = -8$
Let’s substitute the value of $x$ to the equation to get $y$

$y = x^2+ 16x + 64$
$y = (-8)^2+ 16(-8) + 64$
$y= 64-128+64$
$y=128-128$
$y=0$

So our vertex coordinates are
$(-8, 0)$

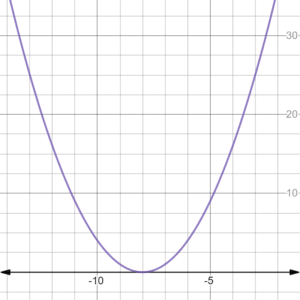
Example 2

$y = 2x^2- 4x - 2$

The axis of symmetry is $x = \dfrac{-b}{2a}$
our values are as follows:
$a = 2$
$b = -4$
$c = -2$

Now, let’s solve for the axis of symmetry

$x = \dfrac{-b}{2a}$
$x = \dfrac{-(-4)}{2(2)}$
$x = \dfrac{4}{4}$
Final answer is

$x = 1$
Let’s substitue the value of $x$ to the equation to get $y$

$y = 2x^2- 4x - 2$
$y = 2(1)^2- 4(1) - 2$
$y= 2-4-2$
$y=2-6$
$y=-4$

So our vertex coordinates are
$(1, -4)$

Video-Lesson Transcript

Let’s go over properties of quadratic functions.

Quadratic functions have this form:

$y = ax^2 + bx + c$

and the more basic for is:

$y = x^2$

The graph looks like a letter “U” and is symmetrical on the $y$ -axis. It can be anywhere in the graph or upside down.

If you look at the line, it starts from the top then goes down and stops at a point then back up again.

The point where it stops and turns the other direction is called a vertex.

Also, the axis of symmetry is through the vertex.

What about when the vertex is not on a particular tick mark?

We might not know the exact numbers.

But of course, there’s a way to solve it algebraically.

Before we get to solving it algebraically, let’s do it first on a calculator.

We have $y = x^2 + 4x - 2$

Let’s look at the graphing calculator.

It goes down then stops and goes back up again.

There’s the vertex – where it goes up and down on the axis of symmetry where it’s a reflector of the other side.

The calculator already identified the values for us.

According to the calculator, the vertex is $(-2, -6)$

Then let’s graph.

The axis of symmetry is $x = \dfrac{-b}{2a}$

Remember that the basic format for quadratic functions is $y = ax^2 + bx + c$ .

So given that our line is

$y = x^2 + 4x - 2$

our values are as follows:

$a = 1$

$b = 4$

$c = -2$

Now, let’s solve for the axis of symmetry

$x = \dfrac{-b}{2a}$

$x = \dfrac{-(4)}{2(1)}$

$x = \dfrac{-4}{2}$

Final answer is

$x = -2$

Now, how do we find the vertex?

The vertex is a point on the graph.

So we could use the function to find out this point.

At this point, we know what is the value of $x$ . So how do we find out the value of $y$ ?

Let’s use the function and substitute the value of $x = -2$ .

$y = x^2 + 4x - 2$

$y = -2^2 + 4 (-2) - 2$

$y = 4 - 8 - 2$

$y = -6$

So our vertex coordinates are

$(-2, -6)$

Just like the answer on the calculator earlier.