Linear Equations | Solve for One Variable in Terms of Another

In this video, we will be learning how to solve for one variable in terms of another in linear equations, such as solving for y in terms of x. After you finish this lesson, view all of our Algebra 1 lessons and practice problems.

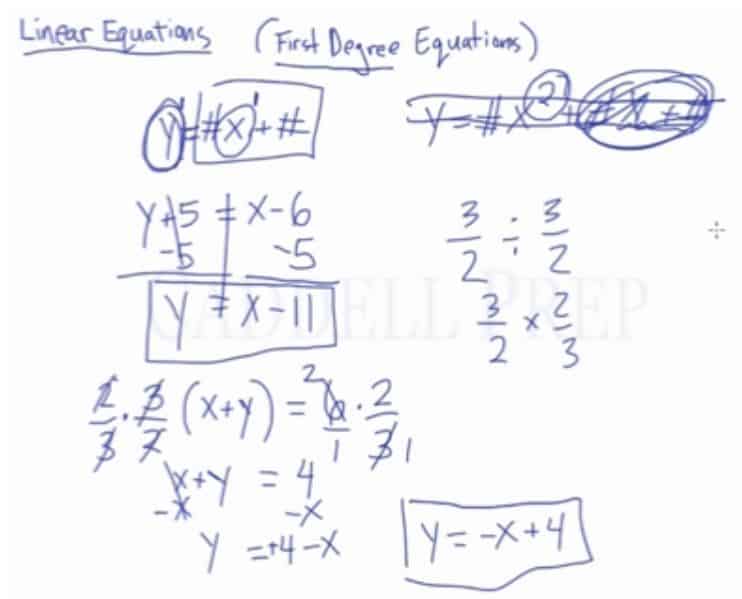
Example of Solving a Linear Equation

$\frac{3}{2}(x+y)=6$

$\frac{3}{2}(x+y)\cdot\frac{2}{3}=6\cdot\frac{2}{3}\leftarrow$ Multiply both sides by $\frac{2}{3}$ to isolate x and y

$(x+y)-x=4-x\leftarrow$ Subtract x from both sides to isolate y

$y=-x+4\leftarrow$ Write in $y=mx+b$ form

Example 1

$\dfrac{y}{2}-8x=6$

First, we must get rid of $\dfrac{1}{2}$ . So, we multiply it by its reciprocal.

$2(\dfrac{y}{2}-8x)=(6)(2)$

$y-16x=12$

Let’s add $16x$ to both sides to keep the format $y=ax+b$

$y-16x+16x=12+16x$

Therefore,

$y=16x+12$

Example 2

$3(6x+3y)=9$

First, distribute $3$ to each of the terms inside the parenthesis

$3(6x)+3(3y)=9$ $18x+9y=9$

Then, subtract $18x$ to both sides

$18x+9y-18x=9-16x$ $9y=-18x+9$

We have to get rid of $9$ in $9y$ to keep the format $y=ax+b$

So, we multiply it by its reciprocal

$\dfrac{1}{9}(9y)=(-18x+9)\dfrac{1}{9}$

Therefore,

$y=-2x+1$

Video-Lesson Transcript

In this lesson, we’ll go over linear equations also known as first degree equations.

The basic format of a linear equation is

$y = ax + b$ , where $a$ and $b$ are numbers.

The first thing is that we have two variables $y$ and $x$ .

A very important reminder about linear equation is why it’s called first-degree equation.

It’s because the exponent for the variables – $y$ and $x$ – is $1$ .

So if we have this equation:

$y = ax^2+b$

The end of the equation doesn’t matter at this point.

As soon as you see an exponent that isn’t 1 it’s not a linear equation.

The exponent has to be one.

So, what we really want to do in a linear equation is to solve for one of the variables.

So what we want is some variable such as $y$ equals everything else. Whatever that everything else is.

For example:

$y + 5 = x - 6$

What you need to do is to isolate $y$ by itself.

So, we have to do inverse operations or reverse PEMDAS to get $y$ by itself.

Don’t worry about the fact that there’s $x$ here. It’s just a number minus another number. This doesn’t matter.

The only thing that we want to focus on is $y$ .

So let’s isolate $y$ by subtracting $5$ from both sides of the equation.

$y + 5 - 5 = x - 6 - 5$

Our final answer is

$y = x - 11$

Let’s try another one.

$\dfrac{3}{2} (x + y) = 6$

What we’re going to do here is to get rid of $\dfrac{3}{2}$ .

To do this, we just have to multiply it by it’s reciprocal. It cancels out perfectly.

$\dfrac{2}{3} \dfrac{3}{2} (x + y) = 6 \times \dfrac{2}{3}$

A side note:

The reason why we multiplied it by its reciprocal is because we want to divide the fraction to cancel it out.

What is $\dfrac{3}{2} \div \dfrac{3}{2}$ ?

We have to do keep-change-flip. So we have

$\dfrac{3}{2} \times \dfrac{2}{3}$

So by multiplying by reciprocal, I actually am dividing.

Let’s move on solving

$x + y = \dfrac{6}{1} \times \dfrac{2}{3}$

Maybe you want to put a denominator to $6$ , so we can cross cancel.

So now we have

$x + y = 4$ $y = 4 - x$

This is okay but we want to write $x$ -term first.

So our final answer is

$y = -x + 4$