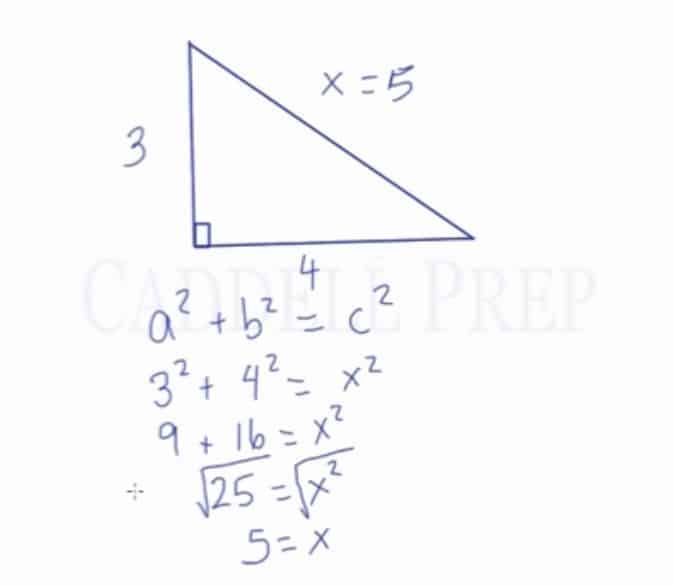
Learn Pythagorean Theorem | Solve For A Missing Side In A Right Triangle

In this video, we are going to look at how to find a missing side length of a right triangle by using the Pythagorean Theorem. After you finish this lesson, view all of our Pre-Algebra lessons and practice problems.

Pythagorean Theorem
$a^2+b^2=c^2$
where a and b are lengths of legs of the right triangle,
and c is the length of the hypotenuse.

For example:
To solve the following equation:
$a^2+b^2=c^2$

Substitute the variables where 3 replaces a and 4 replaces b
$3^2+4^2=x^2$

Solve for $3^2$ and $4^2$
$9+16=x^2$

Add the 9 and the 16 together, leaving us with:
$25=x^2$

Find the square roots on both sides
$\sqrt{25}=\sqrt{x^2}$

Leaving us with:
$5=x$
So the hypotenuse equals to 5

Examples of Pythagorean Theorem

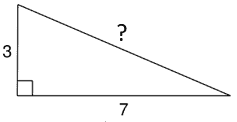
Example 1

Use the pythagorean theorem equation

$a^2+b^2=c^2$

Substitute the variables where $3$ replaces $a$ and $7$ replaces $b$

$3^2+7^2=x^2$

Solve for $3^2$ and $7^2$

$9+49=x^2$

Add the $9$ and the $49$ together, leaving us with:

$58=x^2$

Find the square roots on both sides

$\sqrt{58}=\sqrt{x^2}$ $7.62=x$

So the hypotenuse equals to $7.62$

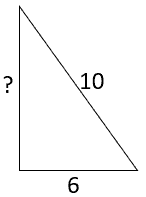
Example 2

Use the pythagorean theorem equation

$a^2+b^2=c^2$

Substitute the variables where $6$ replaces $a$ and $10$ replaces $c$

$6^2+b^2=10^2$

Solve for $6^2$ and $10^2$

$36+b^2=100$

Subtract $36$ from $100$ , leaving us with:

$b^2=64$

Find the square roots on both sides

$\sqrt{b^2}=\sqrt{64}$ $b=8$

So, $b$ is equals to $8$

Video-Lesson Transcript

In this lesson, we’ll discuss the Pythagorean Theorem.

It’s very important to note that Pythagorean theorem is only for right triangles. You can not use this theorem in other types of triangles.

A right triangle has a $90^{\circ}$ angle.

Let’s go over some terminologies first.

The side opposite of the right angle is called hypotenuse.

The other two sides are known as legs.

Given this right triangle, there is an equation that relates the measurement of the legs to the measurement of the hypotenuse.

This equation is simply

$a^2 + b^2 = c^2$

Where hypotenuse is $c$ and the legs are $a$ and $b$ .

As for the legs, it doesn’t matter which side you put in as $a$ or $b$ . It’s your call.

This equation is called the Pythagorean theorem.

Let’s have an example and put this equation to work.

Here’s a right triangle with a vertical leg measuring $3$ and a horizontal leg measuring $4$ . And the hypotenuse is unknown or $x$ .

Let’s start off with our equation

$a^2 + b^2 = c^2$

Again, as it doesn’t matter which leg is $a$ or $b$ .

Let’s just pick the vertical leg to be $a$ and the horizontal leg to be $b$ .

$3^2 + 4^2 = x^2$ $9 + 16 = x^2$ $25 = x^2$

To solve the value of $x$ , we have to do the inverse operation which is squareroot.

$\sqrt{25} = \sqrt{x^2}$ $5 = x$

So our hypotenuse is $= 5$