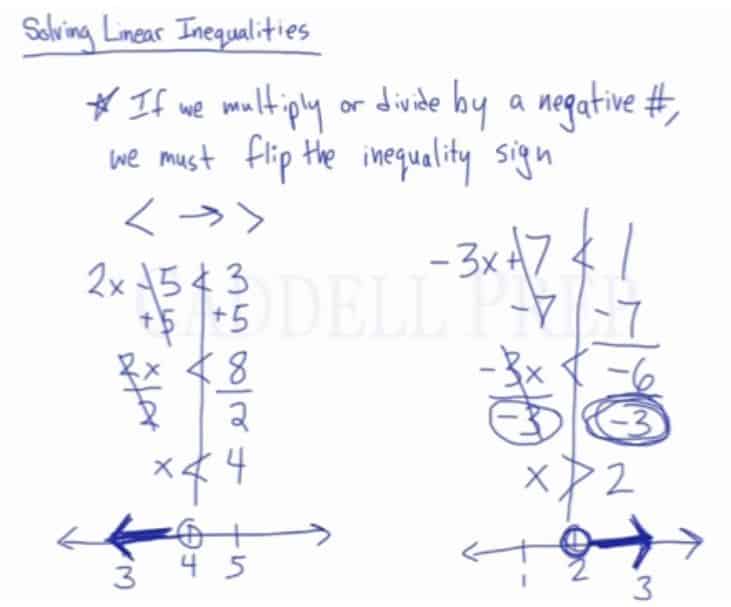In this video, we will be learning how to solve linear inequalities. After you finish this lesson, view all of our Algebra 1 lessons and practice problems.
For Example:
First we split the inequalities:
Example 1
First we split the inequalities:
Example 2
5x+3\leq18
First, subtract 3 on both sides
5x+3-3\leq18-3
5x\leq15
Then, divide 5 on both sides to isolate x
\dfrac{5x}{5}\leq \dfrac{15}{5}
x\leq 3
Video-Lesson Transcript
In this lesson, we’ll go over solving linear inequalities.
This is very similar to solving linear equations except for one thing:
If we multiply or divide by a negative number, we must flip the inequality sign.
So a sign like this could be flipped the other way and become this
.
Let’s look at an example:
So let’s just treat the inequality sign as a regular equal sign as we solve.
First, let’s add on both sides.
From here we have to divide by to isolate the
.
And we end up with
This is our answer.
So if we need to graph it, let’s draw a number line and draw an open circle at . Open circle because
is not equal to
. Then make an arrow going to the left.
Next, we have
Again, we’re going to treat it as a regular equation when solving .
First thing we have to do is to get rid of , so we subtract
on both sides.
Then let’s solve for by dividing by
.
And because we’re dividing by , we have to flip the inequality sign.
Our answer is
Remember, when we divide by a negative number, we always have to flip the sign.
It doesn’t matter if the dividend is positive or negative. All we care about is when the divisor is negative, that’s the time we flip the sign.
If we graph the answer, let’s draw a number line.
Draw an open circle at number . It’s not a filled circle because it is not equal to.
Since is greater, draw a line going to the right.
Again, solving inequalities is very similar to solving regular equations except if we multiply or divide by a negative number we have to flip the sign.
Another difference is that we’re not going to have an explicit answer for or an explicit solution for
. It’s going to be a range of numbers.
We won’t have is equal to a number.
Our answer is is any number less than or greater than a number. All the way up to infinity.
Here we have a more complicated inequality.
We have two different conditions.
and
What we should do is separate this into two different inequalities.
and
Let’s solve the inequality on the left first.
Let’s add on both sides.
Then solve by dividing by
.
Now, let’s solve the other inequality.
Let’s start by adding on both sides.
Then solve for by dividing both sides by
.
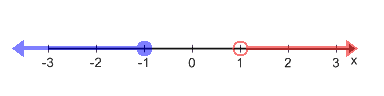
Let’s draw a number line to graph these two inequalities starting with and ending in
.
For , we have to draw an open circle at number
. Open circle because it is not equal to. And since it’s greater than, draw a line going to the right.
Now for , so let’s draw a shaded circle at
since it’s also equal to it. Then draw a line going to the left.
Further, draw a line to the other circle.
Now this line segment represents our solution.
Our answer can also be written as:
Notice that the two endpoints are the end numbers as well – and
.
And is somewhere in between these two numbers but can also be equal to
.
Let’s have another complex inequality.
Let’s break this down into two simple inequalities.
and
Let’s work on the first inequality by adding on both sides.
To solve , divide both sides by
.
Now, let’s solve the other inequality.
Let’s start off by adding on both sides.
To solve for , we’ll divide both sides by
.
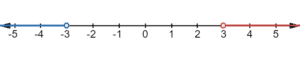
So, now we graph this by drawing a number line.
Draw an open circle at since it’s not equal to. Then draw a line going to the right since
is greater than
.
Next, draw a shaded circle at because
could equal to it. Then draw a line going to the left since
is less than
.
The two arrows are pointing in different directions.
Now, we can write our solution as
or
won’t be able to satisfy both, so we write “or”.