Learn about the relationship between parallel and perpendicular lines. After you finish this lesson, view all of our Algebra 1 lessons and practice problems.
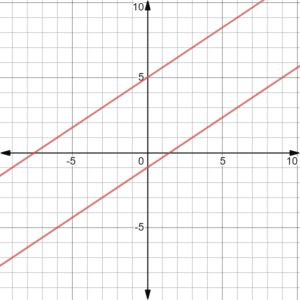
Parallel lines have the same slope but different y-intercepts. Ex: and
are parallel.
Perpendicular lines have slopes that are the negative reciprocals of each other and may or may not have the same y-intercept. Ex: and
are perpendicular.
Examples of Parallel And Perpendicular Lines
Example 1
Both have the same slope which is
Therefore, the lines are parallel to each other.
Example 2
The slopes are negative reciprocals of each other
Therefore, the lines are perpendicular.
Video-Lesson Transcript
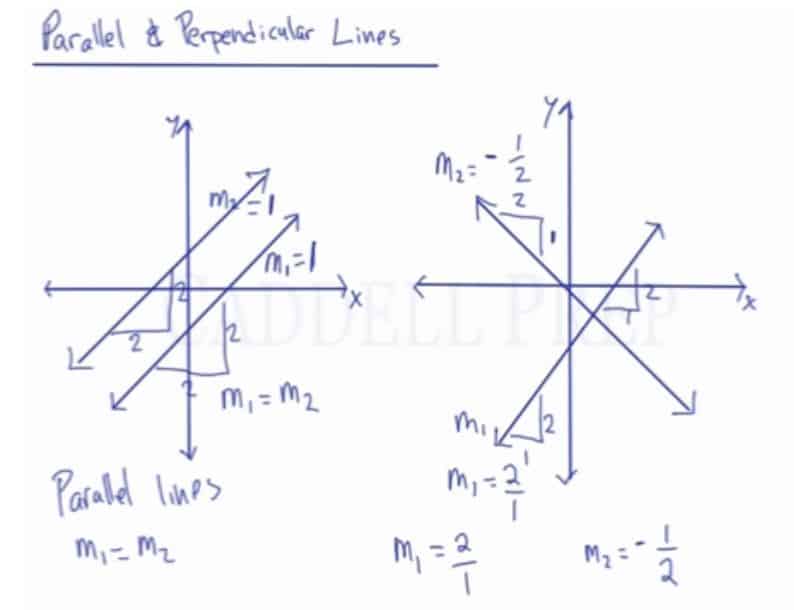
Let’s go over parallel and perpendicular lines.
We have two graphs each with a line.
The one on the left side has a positive slope. The line is going upwards from left to right.
If we draw a line parallel to it, it would look something like this.
If the first line is going to run over and rise at
, then the second line will show the same exact rate.
So, if the slope of the first line is and the slope of the second line is
, we can say that
.
So if then we can say that
.
Now, let’s look at the second graph.
Let’s say that this line is over and up
, the slope here is
.
Now if we draw a line perpendicular with this, it will look something like this.
The thing with a perpendicular line is that it goes the other way. If the first line is going up, then the perpendicular line goes down. If one line has a positive slope, then the other line has a negative slope.
Now if the first line over and up
, the perpendicular line is going over
and down
.
So the slope of the second line is
Let’s look at these closely.
These two slopes are the negative reciprocal of each other.
Therefore, in parallel lines the slopes are equal .
While the perpendicular line is the negative reciprocal of each other.