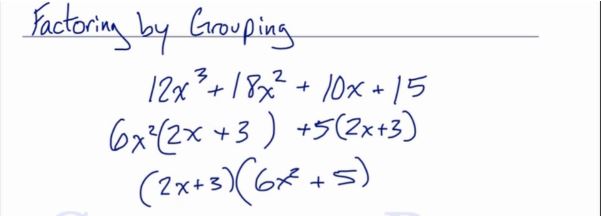In this video, we are going to look at how to factor by grouping. After you finish this lesson, view all of our Algebra 1 lessons and practice problems.
For example:
To factor
, first think about it in two pieces, cutting it in half. Then we will look at the first two terms, and take out the greatest common factor, which is 
. This will leave us with
Then, we do the same thing for the next two terms. The greatest common factor here is 5. When we take out the greatest common factor, we are left with
Notice that the same exact factors are written in both sets of parentheses. From here we can factor out the
from each term. This will result in a final answer of
Examples of Factoring by Grouping
Example 1
Factor 
Group the first two terms together and then the last two terms together.
Factor out a GCF from each separate binomial.
x^2(x+7)+x^2(x+7)
Factor out the common binomial.
(x+7)(x^2+2)
Example 2
Factor 
Group the first two terms together and then the last two terms together.
Factor out a GCF from each separate binomial.
Factor out the common binomial.
Video-Lesson Transcript
Let’s go over factoring by grouping.
We have 
So we’re going to factor this four-term polynomial by grouping.
We’re going to split this in half.
Let’s look at the first two terms of the polynomial.
And we’ll find out what is the greatest common factor of these two terms.
It’s .
Let’s factor.
Now let’s do the same with the other two terms.
The greatest common factor for these two is 
.
Let’s factor.
Let’s put the plus sign.
At this point, we have the same exact factors:
We can actually factor this out of both of these terms.
We have
So let’s take the same factors out.
Our final answer is
Let’s take a look at another example.
Again, let’s split the polynomial into two.
Then factor the first two terms first.
There’s no greatest common factor for these two coefficients. The only factor we have is the variable.
Then do the same with the remaining two terms.
goes into both of these but since they are negative, we would want to take the negative out.
So now we have
Let’s take the common factor out. And we’re left with our final answer.
This is polynomial factoring.
