Learn how to calculate slope from a graph and from a pair of coordinates. Learn about the different types of slope- positive slope, negative slope, zero slopes (no slope), and undefined slope. After you finish this lesson, view all of our Pre-Algebra lessons and practice problems.
Examples of Slope
Example 1
Determine the slope of the line passing through the points and
.
Let’s use this formula and substitute the given
Example 2
Determine the slope of the line passing through the points and
.
Let’s use this formula and substitute the given
Video-Lesson Transcript
In this lesson, you’ll learn all about slopes.
It tells us how steep a line is. And how quickly it goes up or how quickly it goes down.
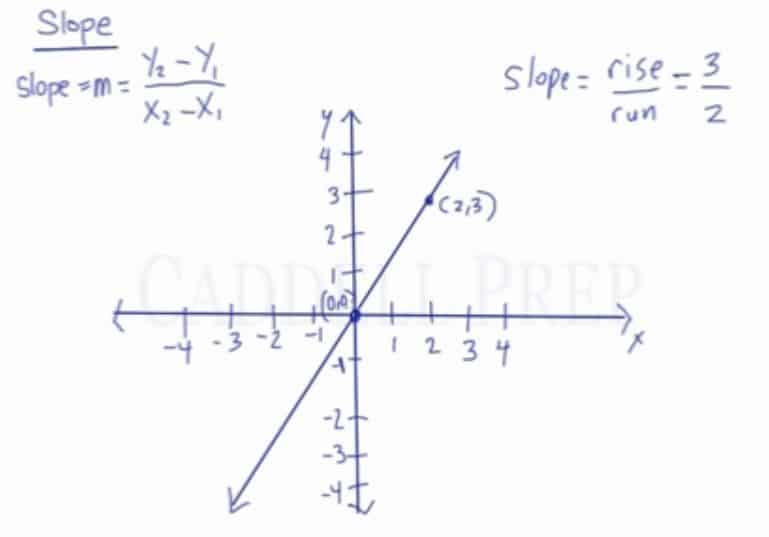
We can simply put it as .
Whereas rise is how high it goes up and run is how far it is from the origin.
Here we have a point with coordinates and the origin has
coordinates.
We can count how high the slope is using the graph.
Here we have and
So our slope is .
But we can also determine it without using the graph.
Let’s use this formula:
This makes sense because the change in -coordinates will tell us how high it goes and the change in
-coordinates will tell us how far over it runs.
runs horizontally and
is vertical.
So, let’s go back to our example of a point with coordinates and the origin has
coordinates.
Let’s use the formula and substitute the given
Again, we got the same answer. Either we use the graph or the formula.
Different Types of Slope
Now let’s take a look at different types of slopes.
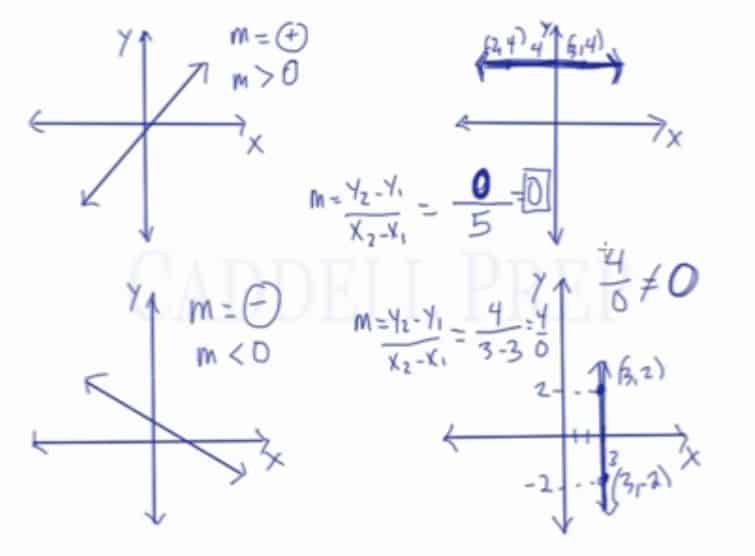
The first one we see goes from left to right upwards.
This is called a positive slope . Or we could also say that the slope is greater than
.
The second one we have goes from left to right downwards.
This is called a negative slope . Or we could say that the slope is less than
.
This third one is a straight horizontal line. This is a strange slope.
Remember the formula for slope?
When we pick any two points, there’s one and the same -coordinate. So if we subtract the numerator, our answer is
. So the slope is also
. Remember that
divided by any number is
.
Thus, we call this zero slope.
The last one we have is straight vertically. If the third one is strange, this one is even more peculiar.
Using the same logic as the third, let’s pick any two points. Here, our -coordinate is the same since it’s vertically straight line. Using the formula, our denominator is
.
Very important to note that
Remember, any number divided by does not exist.
Thus, we call this an undefined slope.
So just to recap, there are four types of slopes.
It is positive when the line from left to right goes upwards.
Negative when the line from left to right goes downward.
Zero when the line is straight horizontally.
And undefined when the line is straight vertically.