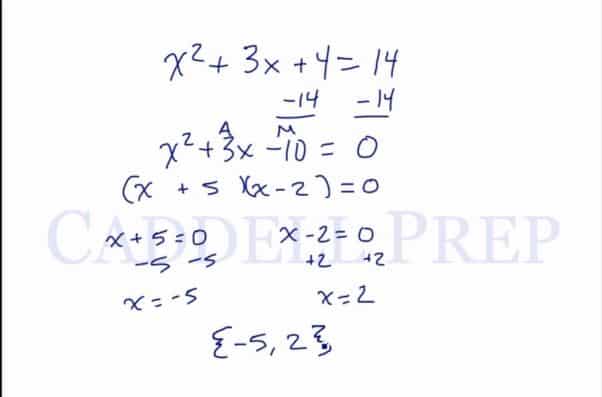In this video, we are going to look at solving quadratic equations by factoring. To solve equations by factoring, we must make sure that the quadratic is set equal to 0. After you finish this lesson, view all of our Algebra 1 lessons and practice problems.
For example:
If we are given the equation
we can first factor like normal. We need two numbers that add up to 5 and multiply to 6. These two numbers are 2 and 3. So we are left with
Now if we think about this logically, for two numbers to multiply together to give us 0, then at least one of these numbers must be 0. This means that either x+2 must equal 0 or x+3 must equal 0. So if we set each equal to 0 we get
and
When we solve both of these by simply subtracting 2 and subtracting 3, we get that
If we had something more complicated like
then the first step would be to subtract the 14 from both sides to make sure that our equation is set equal to 0. So now we are left with
From here we can factor and solve. Two numbers that add up to 3 and multiply to -10 are 5 and -2, so
From here, we set each factor equal to 0
and
and solve by subtracting 5 and adding 2 to get
Examples of Solving Equations by Factoring
Example 1
What are the solutions to ?
Let’s write two parenthesis and an in each parenthesis.
Then think of two numbers that when you add up will equal and when multiplied will equal
We have to come up with one of these terms be zero.
and
and
Our two solutions are
Example 2
What are the solutions to ?
Let’s write two parenthesis and an in each parenthesis.
Then think of two numbers that when you add up will equal and when multiplied will equal
We have to come up with one of these terms be zero.
and
and
Our two solutions are
Video-Lesson Transcript
Let’s go over how to solve equations by factoring.
The first thing to note here is that we have a quadratic and it’s equal to zero.
So we have to make sure that the right side is zero.
Now, let’s factor this.
Draw two parenthesis and write on each.
Then find two numbers that will add up to and when multiplied will be equal to
.
When can two numbers when multiplied be equal to zero?
One of them has to be zero. Because of zero product property.
So we have to come up with one of these terms be zero.
Meaning or
Either of the two should be zero.
,
,
and
,
,
So we have two solutions:
{}
We usually use the brackets not the parenthesis.
Let’s have another one
Again, let’s factor this.
Draw two parenthesis and in each parenthesis.
Then think of two numbers that when you add up will equal and when multiplied will equal
.
,
,
,
,
and
,
,
Our two solutions are
{}
Take a look at this one:
Notice that the right side is not zero.
So we have to make it zero.
,
Now we can factor this out.
,
Let’s solve for
,
,
and
,
,
So our solution set is
{}