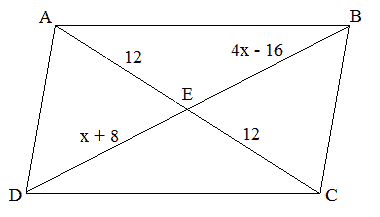
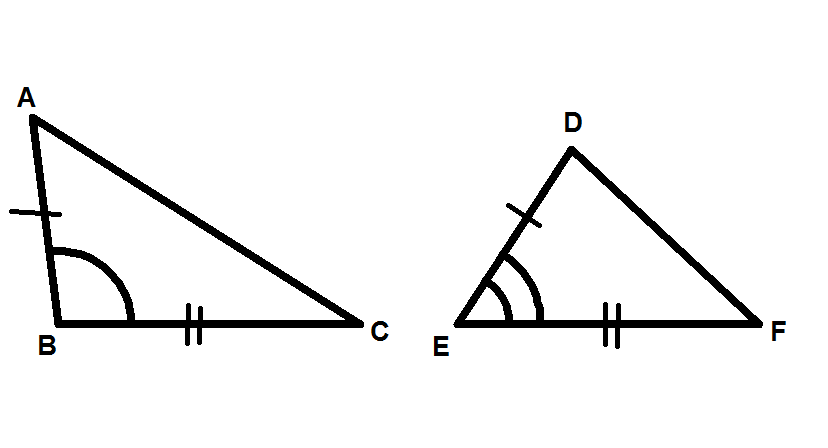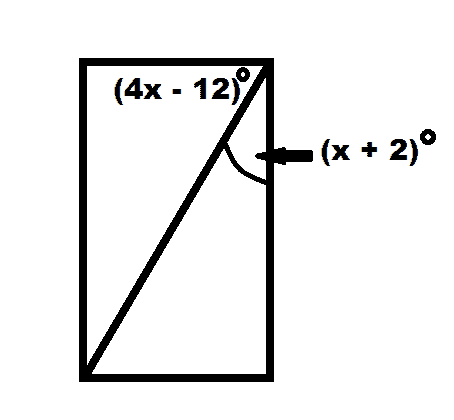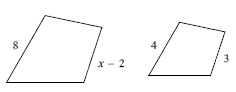Go through the lessons and practice problems below to help you learn Geometry and excel in school. We’ll track your progress and help you identify your strengths and weaknesses. Our geometry lessons is available to everyone, but you need to create an account in order to access the practice questions and track your progress.
Geometry: 01-Parallel and Perpendicular Lines
Geometry: 02-Congruent Triangles
Geometry: 03-Relationships with Triangles
Geometry: 04-Polygons and Triangles
Geometry: 06-Right Triangles and Trigonometry
Geometry: 07-Transformations
Geometry: 08-Area
Geometry: 09-Surface Area and Volume
Geometry: 10-Circles
I. Parallel and Perpendicular Lines
Lesson: Properties of Parallel Lines
Example: Identify each pair of angles as corresponding, alternate interior, alternate exterior, same-side interior, vertical, or adjacent.
Lesson: Proving Lines Parallel
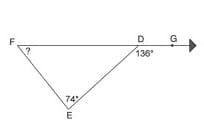
Example: Find the measure of the indicated angle that makes the two lines parallel.
Lesson: Triangle Angle Sum and Exterior Angle Theorem
Example:Find the measure of each angle indicated.
Lesson: Equations of Lines in the Coordinate Plane
Example: Sketch the graph of the line
Lesson: Writing Equations of Parallel and Perpendicular Lines
Example: Write the slope-intercept form of the equation of a line that passed through (3, 4) and is parallel to .
II. Congruent Triangles
Lesson: Congruent Triangles
Example: State if the two triangles are congruent. If they are, state how you know.
Lesson: Triangle Congruence by SSS and SAS
Example: State is the two triangles below are congruent, and if so state how you know.
Lesson: Triangle Congruence by ASA and AAS
Example: State is the two triangles below are congruent, and if so how?
Lesson: Identifying Corresponding Parts of Congruent Triangles
Example: Give that triangle ABC is congruent to triangle DEF, which pair of angles are congruent?
Lesson: Isosceles and Equilateral Triangles
Example: In ,
Which of the following statements is true?
Example: In ,
. If the measure of
is 50 degrees, and the measure of
is
degrees, what is the value of
?
Lesson: Triangle Congruence by HL (Right Triangles)
Example: State is the two triangles below are congruent, and if so how?
Lesson: Congruence in Overlapping Triangles
Example: Given: , what postulate will prove
?
III. Relationships with Triangles
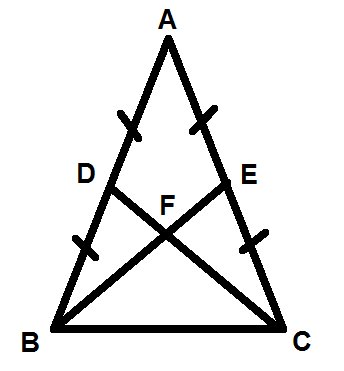
Midsegments of Triangles
Example: Find the length of VU
Angle Bisectors in Triangles
Example: Find the missing length indicated.
Bisectors in Triangles
Example: Find the measure of the indicated length.
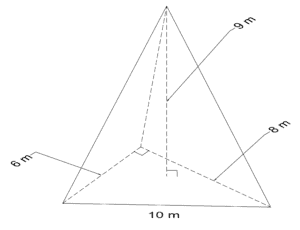
Medians and Altitudes
Example: What is the measure of ?
Indirect Proofs
Example:What is the first step to this indirect proof?
is acute
Lesson: Inequalities in a Triangle
Example:Order the sides of each triangle from shortest to longest.
Inequalities in Two Triangles
Example:
What theorem can be used to prove ?
IV. Polygons and Triangles
Lesson: Angle Sum Theorem for Convex Polygons
Example: What is the interior angle sum of a regular hexagon?
Lesson: Properties of Parallelograms
Example: Find the measurement indicated in the parallelogram.
Proving that a Quadrilateral is a Parallelogram
Example: Given that ABCD is a parallelogram, what is the value of ?
Properties of Rhombuses, Rectangles, and Squares
Lesson: Rhombuses
Lesson: Rectangles
Lesson: Squares
Example: Which figure below is a rhombus?
Conditions of Rhombuses, Rectangles, and Squares
Example: What value of in the figure below would make the figure a rectangle?
Trapezoids and Kites
Polygons in the Coordinate Plane
Example: Triangle ABC has vertices at points (2, 4), (5, 7) and (3, 6). Determine what type of triangle ABC is.
Applying Coordinate Geometry
Example: Is a quadrilateral with vertices (-A, 0), (0, A), (A,0) and (0, -A) a square?
Proofs Using Coordinate Geometry
Example: Which theorem can be used to proved ?
Solving Proportions
Example: Solve for
Similar Polygons and Proportions
Example: Solve for
Proving Triangles Similar
Example:Given , which theorem can be used to prove
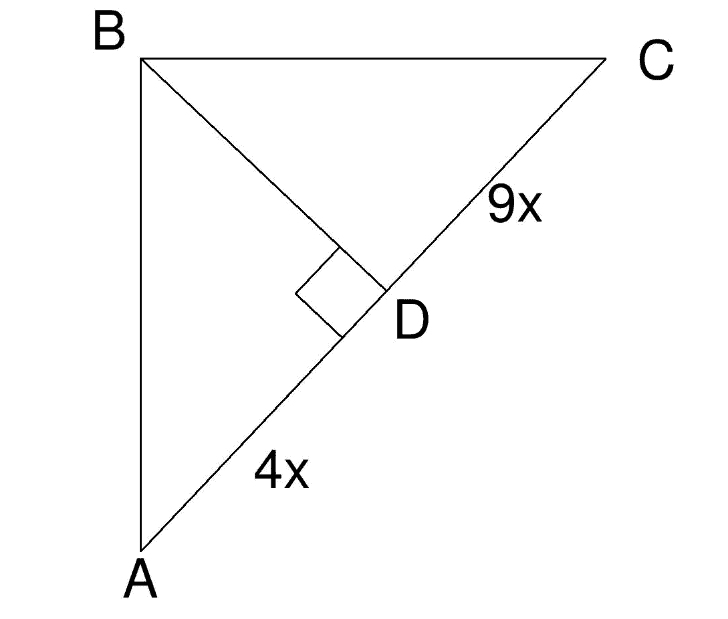
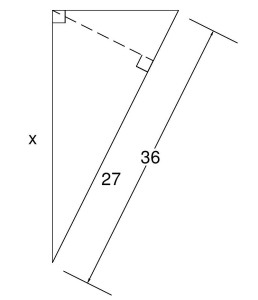
Similar Right Triangles
Example: Solve for
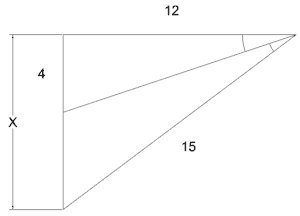
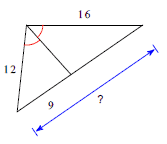
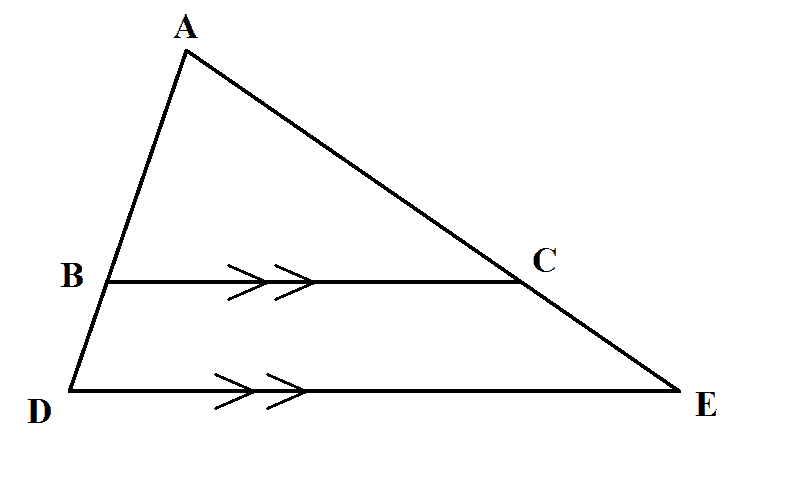
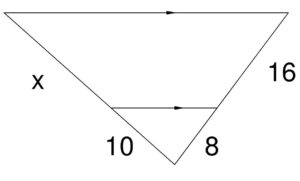
Proportions in Triangles
Example:Find the missing length indicated
VI. Right Triangles and Trigonometry
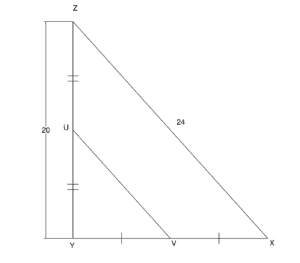
Lesson: Pythagorean Theorem
Example: The hypotenuse of a right triangle has a length of 26 inches. One of its legs is 24 inches. What is the length of the other leg?
Special Right Triangles
Lesson: 30-60-90
Lesson: 45-45-90
Lesson: Pythagorean Triples
Example: A right triangle with an angle of measure 45 degrees, has a hypotenuse of length 13. What are the lengths of the other legs?
Lesson: Trigonometry
Example: Right triangle has the following side lengths:
is 8 ft,
is 3 ft. What is tan(A)?
Elevation and Depression
Example: The height of the Empire State Building is 1,050 feet. At the bottom, there is a basketball 450 feet away. Find the angle of depression from the top of the tower to the basketball.
Law of Sines
Example: In , the length of
is 12 yd, the length of
is 24 yd, and the measure of angle A is 30 degrees. What is the measure of angle B?
Law of Cosines
Example: In , the length of
is 11.3 yd, the length of
is 19.9 yd, and the measure of angle C is 112.4 degrees. What is the length of
?
VII. Transformations
Lesson: Translations
Example: has coordinates A (3, -1), H (5, -1), and F (1,-3). If
is translated 1 unit left and 6 units up, what are the coordinates of its image
?
Reflections
Lesson: Reflection Over an Axis
Lesson: Reflection Over a Horizontal or Vertical Line
Lesson: Reflection Over the Line y=x
Example: has coordinates A (2, 4), B (3, 6) and C (-2, -1). If
is reflected across the x-axis, what are the coordinates of its image
?
Lesson: Rotations
Example: has coordinates D (1, 1), E (3, 1) and F (2, 5). If the triangle is rotated 90 degrees about the origin, what are the coordintates of
?
Compositions of Isometries
Example: What are the coordinates of the point after
?
Congruent Triangles and Congruence Transformations
Example:
Lesson: Dilations
Example: Triangle ,
,
becomes triangle
,
,
under a dilation. What would the scale factor be for this dilation?
Similarity Transformation
Example: When equilateral triangle is dilated by a factor of
, what are the corresponding angle measurements of the image triangle?
VIII. Area
Area of Triangles and Parallelograms
Example: What is the area of a parallelogram with a base of 24 ft and a height of 20 ft?
Area of Trapezoids, Rhombuses, and Kites
Example: What is the area of a trapezoid with bases of 3 ft and 6 ft, with a height of 2.2 ft?
Area of Regular Polygons
Example: What is the area of a regular hexagon that has a side of length 14 inches and an apothem of 12.1 inches?
Perimeter and Area of Similar Figures
Example: The ratio of the perimeters of rectangle I to rectangle II is 1:3. If the area of rectangle I is 12 sq. ft., what is the are of rectangle II?
Trigonometry and the Area of Regular Polygons
Example: What is the area of an equilateral triangle with a side length of 6 m?
Arc Measures and Arc Lengths in Circles
Example: Find the measure of arc JK
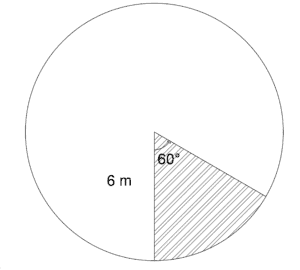
Sector Area
Example: Find the area of each sector.
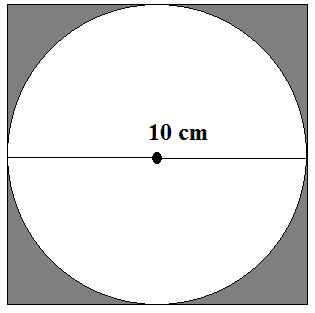
Geometric Probability
Example:A circle is inscribed in a square with the following measurements. What is the probability that a random point will lie in the circle? Leave your answers in terms of if necessary.
IX. Surface Area and Volume
Space Figures and Cross Sections
Example: Use Euler’s fourmula to determine the number of faces of a solid with 9 edges and 5 vertices.
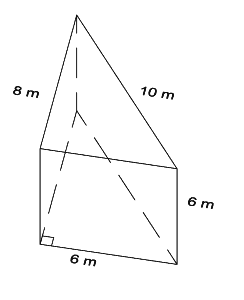
Lesson: Surface Areas of Prisms and Cylinders
Example: Sketch the net of the solid below
Lesson: Surface Areas of Pyramids and Cones
Example:What is the surface area?
Lesson: Volumes of Prisms and Cylinders
Example:Find the volume of each figure. Round your answers to the nearest hundredth, if necessary.
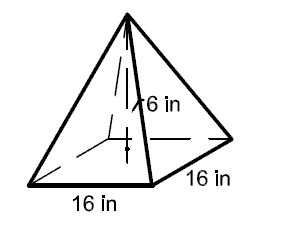
Lesson: Volumes of Pyramids and Cones
Example: Find the volume of the figure below. Round your answers to the nearest hundreth, if necessary.
Lesson: Surface Area and Volume of Spheres
Example: What is the volume of a sphere with a diameter of 18 inches?
Areas and Volumes of Similar Solids
Example: The scale factor between two solid figureds is 2:5. If the surface area of the smaller solid is 45 , what is the area of the larger solid?
X. Circles
Lesson: Tangent Lines
Example: Can a radius be drawn to a point of tangency?
Lesson: Congruent Chords
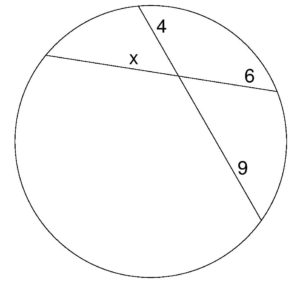
Lesson: Intersecting Chords (Segment Lengths)
Example: Two chords intersect and shown in the diagram below. What is the value of ?
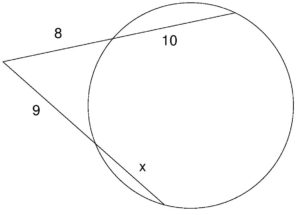
Lesson: Secants and Tangents w/ Vertex Outside of Circle (Segment Lengths)
Example: Solve for in the figure below.
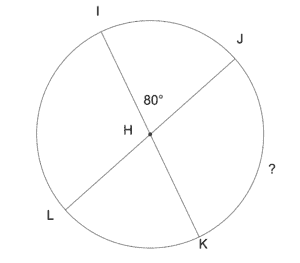
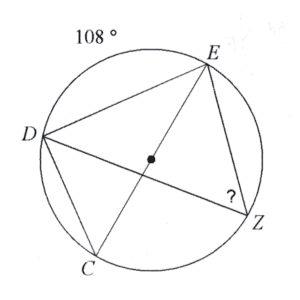
Lesson: Central Angles, Inscribed Angles, and Arcs
Example: Find the measure of the arc or angle indicated.
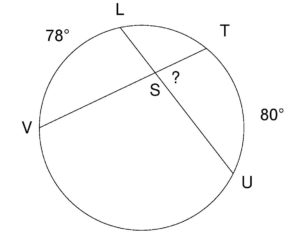
Lesson: Intersecting Chords (Arc and Angle Measures)
Example: Find the measure of the indicated angle formed by the intersecting chords.
Lesson: Tangent and Secant Lines w/ Vertex Outside of Circle (Arcs & Angles)
Example:
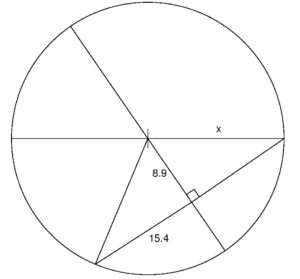
Lesson: Chords Perpendicular to a Radius (Segment Measures)
Example: Solve for .
Lesson: Equation of a Circle
Example: Use the information provided to write the equation of each circle.
Center: (-4, 8)
Radius: 3
Sign up for a free membership on our geometry lessons & start learning today. Learn about the importance of learning geometry here.