Learn Line Segments Formed By A Diameter And Perpendicular Chord

In this lesson, you will learn the relationship that exists between a diameter and perpendicular chord. You will learn the formula to calculate missing measurements of line segments created when a diameter is intersected by a perpendicular chord.

In this video, we are going to look at line segments formed by a diameter and perpendicular chord.
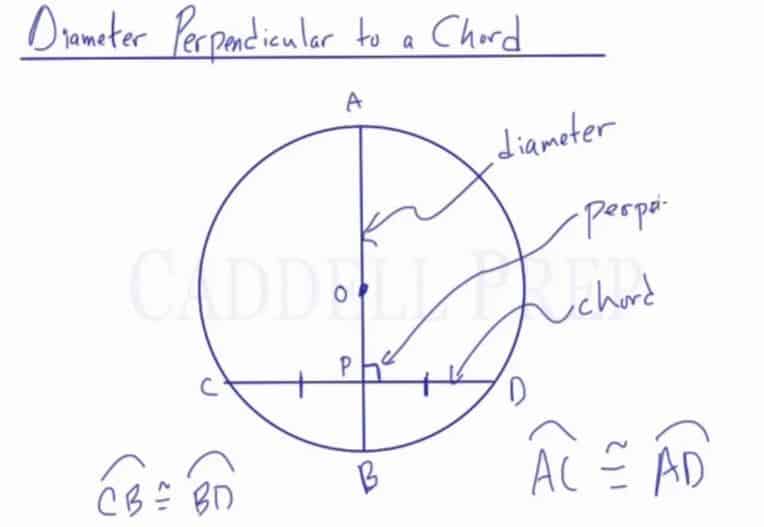
Given circle $O$ , with diameter $\overline{AB}$ , we drew chord $\overline{CD}$ where it intersects the diameter and is perpendicular at point $P$ . When a diameter and a chord intersect in this way, the diameter bisects the chord, so $\overline{CP}$ is the same length as $\overline{PD}$ . The chord does not necessarily bisect the diameter. The arcs are also the same length. In this example, arc $\widehat{BD}$ and arc $\widehat{CB}$ are congruent to each other, and arcs $\widehat{AC}$ and $\widehat{AD}$ are also congruent to each other.

Video-Lesson Transcript

In this lesson, we’ll take a look at diameter drawn that is perpendicular to a chord.

Here, we have circle $O$ and its diameter is drawn.

Now, let’s draw a chord perpendicular to the diameter.

Let’s name the lines.

We have diameter $\overline{\rm AB}$ , chord $\overline{\rm CD}$ and they intersect at point $P$ . It’s perpendicular at point $P$ .

Once the diameter and the chord intersect, the diameter bisects the chord. So, $\overline{\rm CP}$ has the same length as $\overline{\rm PD}$ .

Notice that the chord does not necessarily bisect the diameter. As we can see, $\overline{\rm AP}$ is much longer than $\overline{\rm PB}$ .

But the chord is split in half. It will happen regardless of where we draw the chord. Just as long as it’s perpendicular to the diameter.

Not only these two line segments are the same length, but also the two arcs are of the same length.

$\overset{\frown}{BD}$ and $\overset{\frown}{CB}$ are going to have the same length.

So, we have

$\overset{\frown}{BD} \cong \overset{\frown}{BD}$

We also have $\overset{\frown}{AC}$ and $\overset{\frown}{AD}$ are also congruent.

$\overset{\frown}{AC} \cong \overset{\frown}{AD}$

Very important is that you have to have a diameter, you have to have a chord, and they must be perpendicular to each other.

If that’s the case, we get two pairs of congruent arcs and also the diameter bisects the chord.