Learn About The 45-45-90 Triangles

In this video, we are going to look at 45-45-90 triangles and the ratio that exists among the sides.

What is a 45-45-90 Triangle?

45-45-90 represents the angle measurements of a right triangle. This type of triangle is an isosceles right triangle.

All isosceles right triangles have angles of $45^o$ , $45^o$ , and $90^o$ .

The sides are always in the ratio of $1:1:\sqrt2$ , with the $1$ s corresponding to the lengths of the legs, and the $\sqrt2$ corresponding to the length of the hypotenuse.

Using variables, it can be written as $x:x:x\sqrt2$ . These relationships can be used to find the other sides of the same special triangle when only given one side.

Using the ratio among the sides is an alternative to using Pythagorean Theorem or SOHCAHTOA.

Video-Lesson Transcript

In this lesson, we’ll cover 45-45-90 triangle.

45-45-90 represent the measures of the angles in a triangle. So, we have $45^{\circ}$ , $45^{\circ}$ , and $90^{\circ}$ .

A simple 45-45-90 would be to have the measure of two legs equal to $1$ and the measure of the hypotenuse is $\sqrt{2}$ .

We can test this in Pythagorean theorem and we’ll see that $1^2 + 1^2$ is equal to $\sqrt{2}$ .

Given this triangle, we can draw another similar triangle by multiplying any number to these sides.

If multiplied by $2$ , we’ll get $2$ , $2$ , and $2 \sqrt{2}$ .

Multiplied by $3$ , we’ll have $3$ , $3$ , and $3 \sqrt{2}$ .

Or simply multiply the proportion by $x$ . And we’ll get $x$ , $x$ , and $x \sqrt{2}$ .

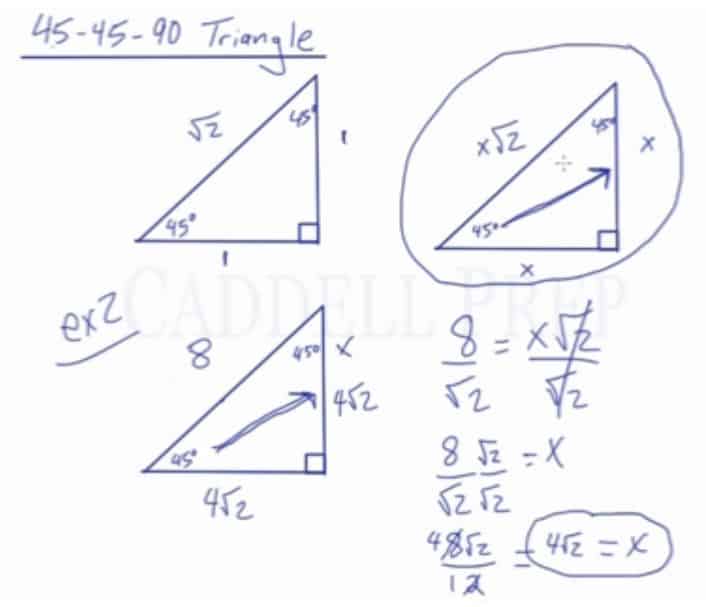
Using this knowledge, we can find the measures of any 45-45-90 triangle if we know one of the sides.

For example:

We have a 45-45-90 triangle and we know that the measure of this side is $5$ then we can find the measure of the other sides.

First, let’s find out what is the value of $x$ .

Take a look at the given.

It’s across from the $45^{\circ}$ angle which is $x$ . So, $5 = x$ .

With that knowledge, we can find the other sides.

The other side which is across from $45^{\circ}$ is also $x$ , so this side is also $5$ .

The hypotenuse matches the $x \sqrt{2}$ . We know that $x = 5$ , so this side is $5 \sqrt{2}$ .

By knowing one of the sides, we were able to find the other sides just by using this diagram.

Let’s look at the second example.

What happens if we’re given the hypotenuse?

Let’s say the measure of this side is $8$ .

The hypotenuse is across from the $90^{\circ}$ and matches up with $x \sqrt{2}$ .

We could set this equal and figure out what $x$ is.

$8 = x \sqrt{2}$

$\dfrac{8}{\sqrt{2}} = \dfrac{x \sqrt{2}}{\sqrt{2}}$

$\dfrac{8}{\sqrt{2}} = x$

But we’re not going to use this because we don’t want a radical sign in the denominator.

We have to rationalize the denominator.

To do that, we have to simply multiply the numerator and denominator by the radical.

$\dfrac{8}{\sqrt{2}} = x$

$\dfrac{8}{\sqrt{2}} \times \dfrac{\sqrt{2}}{\sqrt{2}} = x$

$\dfrac{8 \sqrt{2}}{2} = x$

We can simplify this more into

$4 \sqrt{2} = x$

Now, we can use this to find the other sides.

We can find the side opposite $45^{\circ}$ which is $x$ .

So, this side is $x = 4 \sqrt{2}$

The other side is also $x = 4 \sqrt{2}$ .

It makes sense because this is a 45-45-90 which is isosceles so these two sides have to be the same.

To recap, if we have a 45-45-90 triangle and we were given one of the sides, just match it up with the corresponding side on our diagram then determine what $x$ is and then determine what the other side is.