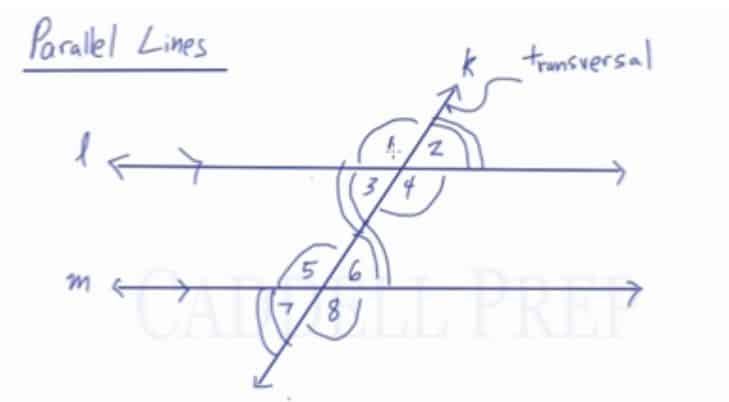
Learn About Parallel Lines And The Angles Formed

In this video, we are going to learn about the relationships among the angles formed when a pair of parallel lines are intersected by a transversal. The angles formed are called vertical, supplementary, alternate interior, alternated exterior, same-side interior, same-side exterior, and corresponding angles.

Here is a list of commonly used terms to describe angles formed by two parallel lines that are cut by a transversal.

Vertical Angles: – Angles formed by intersecting lines; opposite of each other and are also congruent
Supplementary Angles: – Two angles that always add up to $180^\circ$
Alternate Interior Angles: – Angles that are between the two parallel lines, but are on opposite sides of the transversal. They are always congruent.
Alternate Exterior Angles: Angles that are outside on different sides of the two parallel lines, and are on different sides of the transversal. They are always congruent.
Same-side Interior Angles: Angles in between the parallel lines and on the same side of the transversal. They are always supplementary.
Same-side Exterior Angles: Angles that are outside on different sides of the two parallel lines, but are on the same side of the transversal. They are always supplementary.
Corresponding Angles: Angles that match the angles of the opposite parallel line intersection. Graphically, they face the same way and are all always congruent.

Video-Lesson Transcript

In this lesson, we’ll go over angle relationships resulting from two parallel lines cut by a transversal.

We have lines $l$ and $m$ which are parallel to each other.

We also have line $k$ which is the transversal.

When a transversal intersects two parallel lines, there are a lot of angle relationships that result.

First, if we ignore the bottom line and focus on the top line $l$ and transversal $k$ , there are already a lot of angles.

Now if we focus on the bottom line $m$ and transversal $k$ , angles formed here corresponds to the angles formed by the top line.

Angles that corresponds to a group are called corresponding angles. Corresponding angles are congruent. Which means they have the same exact measurement.

Look at the drawing.

Angles $1$ and $5$ are corresponding angles so they are congruent. Meaning they have the same exact measurement.

Therefore, we can say that

$\angle 1 \cong \angle 5$

Likewise, angle $2$ is on the top right as well as angle $6$ .

These two are

$\angle 2 \cong \angle 6$

Now, let’s look at the angle $3$ , which is at the bottom left same as angle $7$ . So, we can say that these two are congruent.

$\angle 3 \cong \angle 7$

Finally, angle $4$ is on the bottom right just like angle $8$ . Which makes them congruent with each other.

$\angle 4 \cong \angle 8$

Corresponding angles are angles that match up on the diagram. Top-left to top-left. Top-right to top-right. And so on.

Let’s go over some more terminologies.

Angles in between the two parallel lines are called interior angles.

Those that are outside of this are known as exterior angles.

If we go from one side of the transversal to the other, that’s called an alternate.

Angles on one side of the transversal are called same-side.

Let’s go over alternate interior angles.

Alternate means the different side of the transversal. While interior means in between the parallel lines.

So, alternate interior angles are $3$ and $6$ . These angles are also congruent.

$\angle3 \cong \angle6$

Angle $5$ and $4$ are also alternate interior angles. This means they are also congruent.

$\angle5 \cong \angle4$

Now, let’s look at alternate exterior angles.

Exterior means outside and alternate means opposite sides of the transversal.

Alternate exterior angles are also congruent.

$\angle 1 \cong \angle 8$

$\angle 2 \cong \angle 7$

Now, let’s take a look at same-side angles.

Same-side interior angles are supplementary.

$\angle3 + \angle5 = 180$

$\angle4 + \angle6 = 180$

Likewise, same-side exterior angles are are also supplementary.

$\angle1 + \angle7 = 180$

$\angle2 + \angle8 = 180$

Now, let’s look at the diagram as a whole.

If you think about it, we’re just jumping back and forth like zigzagging through the diagram.

Angles you jumped into are congruent.

This is the best way to identify congruent angles.

If two angles are not congruent, then they must be supplementary.