Learn About Reflection Over a Horizontal Or Vertical Line

In this video, you will learn how to do a reflection over a horizontal or vertical line, such as a reflection over the line x=-1.

Let’s use triangle ABC with points A(-6,1), B(-5,5), and C(-5,2).

Apply a reflection over the line x=-3

Since the line of reflection is no longer the x-axis or the y-axis, we cannot simply negate the x- or y-values. This is a different form of the transformation.

Let’s work with point A first. Since it will be a horizontal reflection, where the reflection is over x=-3, we first need to determine the distance of the x-value of point A to the line of reflection. We’ll be using the absolute value to determine the distance.
$|-6-(-3)|=|-6+3|=|-3|=3$

Since point A is located three units from the line of reflection, we would find the point three units from the line of reflection from the other side. The y-value will not be changing, so the coordinate point for point A’ would be (0, 1)

Repeat for points B and C. In the end, we found out that after a reflection over the line x=-3, the coordinate points of the image are:

A'(0,1), B'(-1,5), and C'(-1, 2)

Vertical Reflection

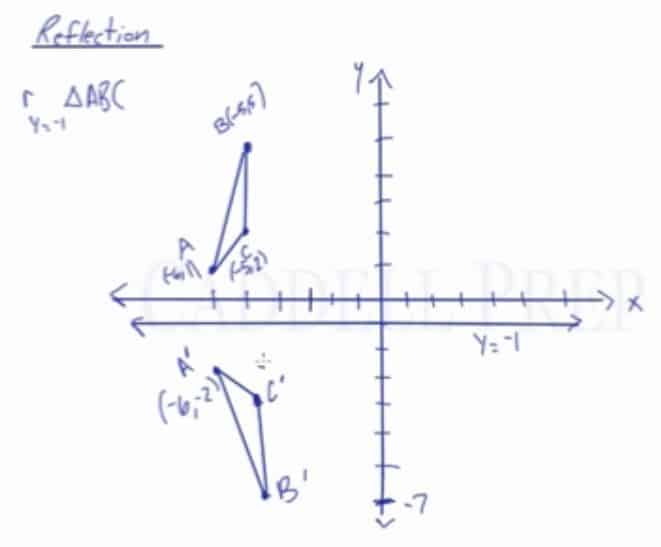
Apply a reflection over the line y=-1

The procedure to determine the coordinate points of the image are the same as that of the previous example with minor differences that the change will be applied to the y-value and the x-value stays the same.

In the end, we would have
A'(-6,-2), B'(-5,-7), and C'(-5, -3)

Video-Lesson Transcript

Let’s say we want to reflect this triangle over this line. A line $x = -3$ rather than the $x$ -axis or the $y$ -axis.

So, we have

$r_{x = -3} \triangle{ABC}$

This line is called $x = -3$ because anywhere on this line $x = -3$ and it doesn’t matter what the $y$ value is.

Graphically, this is the same as reflecting over the $y$ -axis.

We’re just going to treat it like we are doing reflecting over the $y$ -axis. Let’s see how far away it is.

Point $B$ is $2$ units from the line $x = -3$ , so we’re going $2$ units to the right of it. Keep the same height. And we have $B^\prime$ .

Same thing for points $A$ and $C$ .

$C$ is $2$ units away so we’re going to move $2$ units horizontally and we get $C^\prime$ .

Point $A$ is $3$ units from the line so we go $3$ units to the right and we end up with $A^\prime$ .

The reflection of triangle $ABC$ will look like this.

Probably it’s best to do this graphically then get the coordinates from it.

$A^\prime (0, 1)$

$B^\prime (-1, 5)$

$C^\prime (-1, 2)$

Similarly, let’s reflect this over a vertical line.

$r_{y = -1} \triangle {ABC}$

This line represents $y = -1$ because anywhere on this line is $y = -1$ , it doesn’t matter what the $x$ value is.

We’ll treat this the same way as we treat everything so far in reflection.

Point $A$ is $2$ spots away from the $y$ axis so we’ll go $2$ spots below it. And we end up with $A^\prime$ .

$C$ is $3$ spots above the line so we’ll go $3$ spots below it. We end up with $C^\prime$ .

Point $B$ is $6$ spots away so we’ll go $6$ spots below $y = -1$ line.

Now, we can draw a triangle.

We’re able to get the new coordinates graphically by graphing it.

As we look at it, we can now figure out the coordinates.

Looking at the graph, we’ll see that:

$A^\prime (-6, -2)$

$C^\prime (-5, -3)$

$B^\prime (-5, -7)$

A quick sketch easily helps us figure out the coordinates for the image if we reflect triangle $ABC$ over the line $y = -1$ .