Learn About The Arc And Chord Relationships

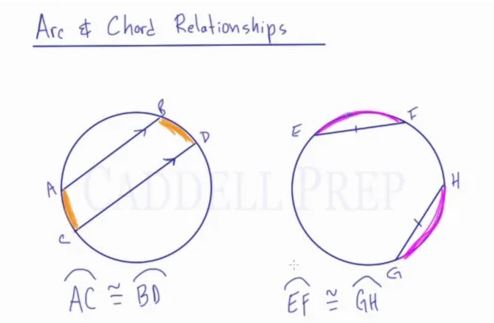
In this video, we are going to look at arc and chord relationships.

Chord: A straight line with both endpoints on the circle.
Arc: Part of a circle’s circumference.

If chord $\overline{AB}$ and chord $\overline{CD}$ are parallel to each other, then the two arcs between are congruent.
If chord $\overline{EF}$ and chord $\overline{GH}$ are the same length, then the two arcs they intercept are congruent.

Video-Lesson Transcript

In this lesson, we’ll go over arc and chord relationships.

We have a circle here and we have a chord $AB$ and chord $CD$ .

If these two chords are parallel to each other, something we know is that these two arcs are congruent to each other.

The arc in between $AB$ and $CD$ are congruent.

$\overset{\frown}{AB} \cong \overset{\frown}{BD}$

Now, in the other circle, we have chord $EF$ and chord $GH$ drawn.

These are not paralleled to each other but these chords are of the same length.

If you have two chords of the same length, regardless of where they’re drawn inside the circle. the arcs that they intercept are going to be congruent to each other.

$\overset{\frown}{EF} \cong \overset{\frown}{GH}$

Just to review arc and chord relationships, when they are parallel, the arcs in between them are congruent. When they are equal in length, the arcs outside of them are congruent.

The vice versa is also true if we were to know that the arcs are congruent.

If $\overset{\frown}{AB} \cong \overset{\frown}{BD}$ then we know that the two chords are parallel.

And if we know that these arcs are congruent, then we also know that the chords are of the same length.