Learn About Dilation | Video Lesson Tutorial

In this video, you will learn how to do a dilation and graph the new image.

Dilation: Transformation of an image that is different in size but proportionate to the original figure.

Dilation Notation:
D_k(x,y) $\rightarrow$ (kx, ky) where k is the scale factor

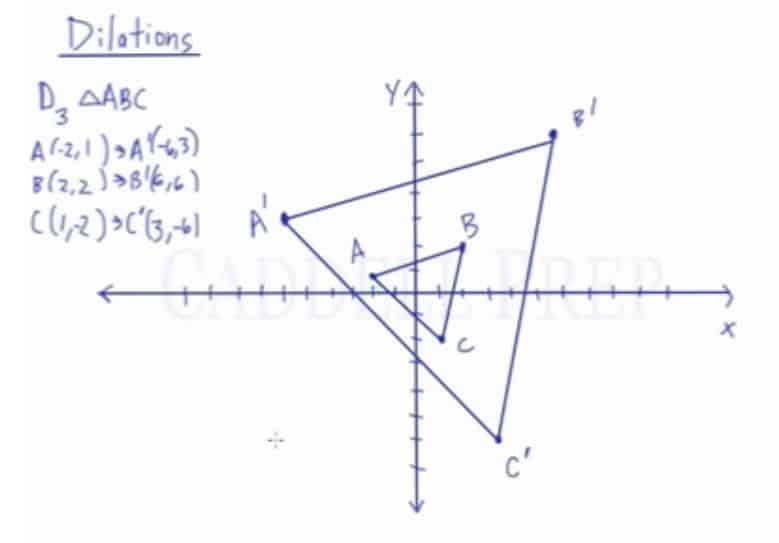
Apply a dilation by a scale factor of 3 to triangle ABC with coordinate points of A(-2,1), B(2,2), and C(1,-2) with the center located at the origin.

Using the dilation notation and the scale factor of 3, we can easily determine the coordinate points of the image by multiplying the x-value by k and the y-value by k.

A(-2,1) $\rightarrow$ A'(-6,3)
B(2,2) $\rightarrow$ B'(6,6)
C(1,-2) $\rightarrow$ C'(3,-6)

Video-Lesson Transcript

Let’s go over dilations.

Dilations are denoted by capital letter $D$ with some number $k$ before whatever it is we’re dilating.

$D_{k} (x, y)$

This $k$ is our factor of dilation or also known as scaled factor.

When we do the scale factor, we just have to multiply all the coordinates by that scale factor.

$D_{k} (x, y) \rightarrow (kx, ky)$

For example,

$D_{4} (2, 5) \rightarrow (8, 20)$

We can see that dilation resulted in a larger coordinate. A larger $x$ value and a larger $y$ value.

If the scale factor is less than one:

$D_{\dfrac{1}{2}} (2, 8) \rightarrow (1, 4)$

Here, the numbers went down.

When we dilate a shape, if $k$ is bigger than $1$ such as $4$ , the shape is going to be bigger.

But if the scale factor is less than $1$ such as $\dfrac{1}{2}$ , then the shape is going to be smaller.

Let’s take this triangle $ABC$ and dialte it with a scale factor of $3$ .

$D_3 \triangle {ABC}$

Let’s first write down our coordinates.

$A (-2, 1) \rightarrow A^\prime (-6, 3)$

$B (2, 2) \rightarrow B^\prime (6, 6)$

$C (1, -2) \rightarrow C^\prime (3, -6)$

We just multiplied all coordinates by $3$ .

Now, let’s graph this.

This is what triangle $ABC$ look like if we have a scale factor of $3$ .

We just simply multiplied the $x$ and $y$ coordinates by the scale factor of $3$ .

Also, $3$ is bigger than $1$ so we expect that the triangle will be bigger.

If the scale factor is less than $1$ then the triangle will be smaller than the original, depending on what the scale factor is.