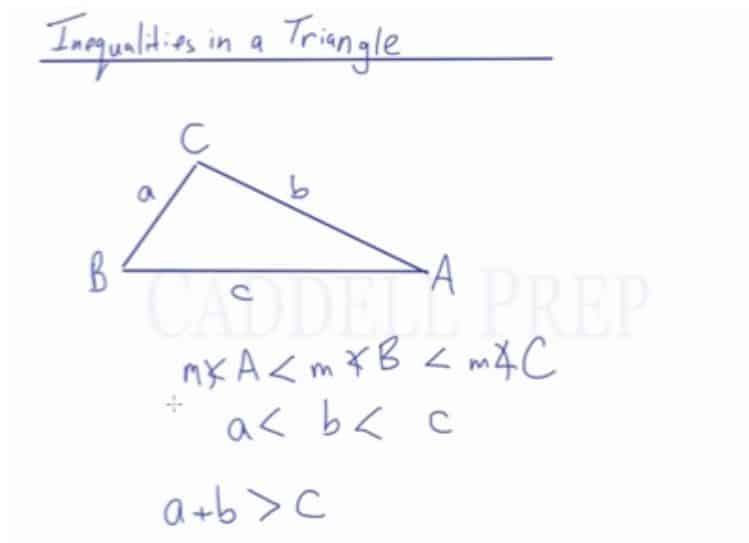
Learn About Inequalities In A Triangle

In this video, we are going to look at inequalities in a triangle that exists among the measures of the angles and the lengths of the sides of a triangle.

First, let’s name the angles A, B, and C. Then, let’s name the sides a, b, and c. The sides and angles correspond to being directly across from one another.

In this diagram, we can see that $m\angle{A} \textless m\angle{B} \textless m\angle{C}$ . The corresponding sides across from the angles are in the same order, so $a \textless b \textless c$ . The two shorter sides MUST add up to equal to a number larger than the longest side, so $a+b \textgreater c$

Video-Lesson Transcript

Let’s go over inequalities in a triangle.

Let’s name these angles $A$ , $B$ , and $C$ .

The side across from angle $A$ we’ll call $a$ . The side across from angle $b$ , we’ll call $b$ . And lastly, the side across from angle $C$ , we’ll call $c$ .

In this diagram, we can see that the measure of angle $A$ is less than the measure of angle $B$ and that’s less than the measure of angle $C$ .

$m \angle A \textless m \angle B \textless m \angle C$

$A$ is the smallest angle, followed by angle $B$ , and $C$ is the biggest angle.

The lines are also in the same order.

Since $A$ is the smallest angle, side $a$ is also the smallest side. Side $b$ is bigger than $a$ . And $c$ is the biggest.

$a \textless b \textless c$

Also other inequality to note is that

$a + b \textgreater c$

In inequality, if $A$ is the smallest angle, the side across from it is also the smallest side.

If $C$ is the largest angle, then the side across from it is also the longest side.

And the sum of the two small sides has to add up to be greater than the longest side.