Learn About Central And Inscribed Angles

In this video, we are going to look at central and inscribed angles:

How to identify central angles
How to identify inscribed angles
The relationship between central angles and the intercepted arc
The relationship between inscribed angles and the intercepted arc

Central Angles: Angles with the vertex located at the center of the circle. The measure of the central angle is the same as the measure of the arc it intercepts.

For example:
If the measure of the central angle is $40\textdegree$ , then the measure of the intercepted arc is also $40\textdegree$ .

Inscribed Angles: Angles with the vertex located on the circumference of the circle. The measure of the inscribed angle is half the measure of the arc it intercepts.

For example:
If the measure of the arc is $40\textdegree$ , then the measure of the inscribed angle is only $20\textdegree$ .

If a central angle and an inscribed angle intercept the same arc, then the central angle is double the inscribed angle, and the inscribed angle is half the central angle.

Video-Lesson Transcript

In this lesson, we’re going to review central and inscribed angles.

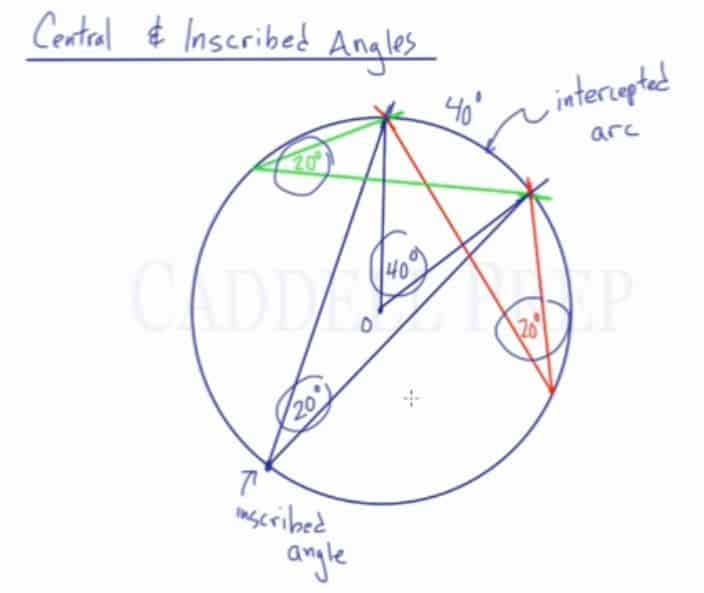
Here, we have a circle with center $O$ .

Let’s draw a radius from the center to the edge of the circle.

We could note that if we go all the way around inside the circle it would be $360^{\circ}$ .

Based on the fact that we can go $360^{\circ}$ inside the circle, we can relate that to the circumference. The entire circumference will be $360^{\circ}$ and any portion of the circumference is some fraction of the $360^{\circ}$ .

The fraction of the circumference is related to the center angle.

If we are to draw another radius and the angle created is $40^{\circ}$ . Then the arc is also $40^{\circ}$ .

This $40^{\circ}$ represents $\dfrac{1}{9}$ of the entire $360^{\circ}$ . The length of the arc is also $\dfrac{1}{9}$ of the total circumference.

The central angle is called central because the vertex is at the center. Whatever the measure of that angle equals the measurement of the arc intercepts in degrees.

Let’s look at the inscribed angle now.

Inscribed angles have their vertex on the circle. The angle drawn is an inscribed angle.

Let’s say that the measure of the arc is $40^{\circ}$ . Then the measure of the inscribed angle is related to that.

Inscribed angles are $\dfrac{1}{2}$ of the arc intercept.

If we can look at how the central angle and inscribed angle is related.

Let’s draw the central angle again. The measure of this angle is $40^{\circ}$ is the same as the arc intercept and the measure of the inscribed angle is $20^{\circ}$ which is half of the measure of the arc it intercepts.

Just focus on the inscribed angle. Its measurement is half of the length of the arc in degrees. As long as it’s inscribed and it intercepts this arc.

For example, we can have an angle at a different location.

This angle is inscribed because its vertex is on the circle and it also intercepts the arc which measures $40^{\circ}$ so the inscribed angle is also $20^{\circ}$ .

If we drew the inscribed angle over here, the measure of this is also $20^{\circ}$ because it intercepts the same arc with $40^{\circ}$ .

What I mean with intercept is if we continue the lines with the angle, we will have an arc in between them. Which is the $40^{\circ}$ arc we’re talking about.

Same thing with the other lines. That is the intercepted arc.

So, whatever the measure of the arc is, the inscribed angle is half.

The measure of the central angle is the same measure of the intercepted arc.

You can see that if a central angle and an inscribed angle intercept the same arc, the central angle would be double the inscribed angles.

Likewise, the inscribed angle is half of the central angle.