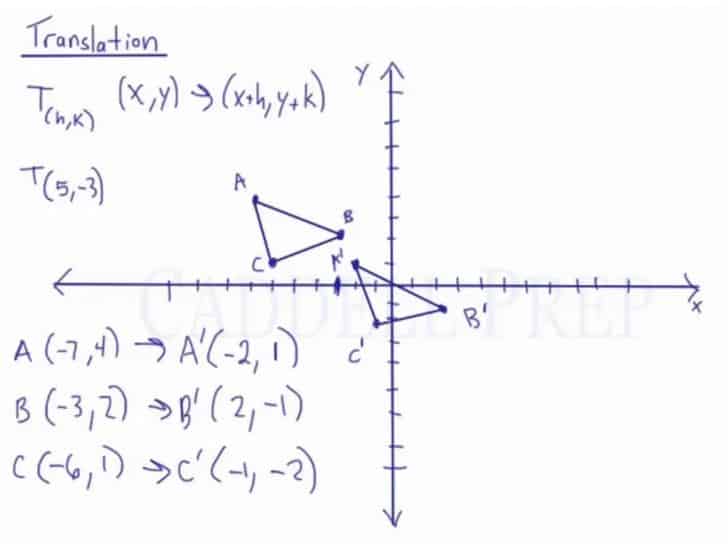
Learn About Translation On The X-Y Plane

In this video, you will learn how to do a translation graphically and then use the coordinates.

Translation: A slide of a slide of a shape on a coordinate plane.
We can move a shape upward, downward, leftward, or rightward.

The notation for translation is T_{(h, k)} where T is the translation, h is the change in the x-axis, and k is the change in the y-axis.

Applying the translation to the coordinate plane, it would be
(x, y) $\rightarrow$ (x+h, y+k)

For example:
A(-7,4)
B(-3,2)
C(-6,1)
with the transformation of T_(5,-3)

Simply combine the values of either the x or the y-axis with the translation notation, and the coordinate points of the image are shown.

A(-7,4) $\rightarrow$ A'(-7+5,4-3) $\rightarrow$ A'(-2,1)
A(-3,2) $\rightarrow$ B'(-3+5,2-3) $\rightarrow$ B'(2,-1)
A(-6,1) $\rightarrow$ C'(-6+5,1-3) $\rightarrow$ C'(-1,-2)

Furthermore, to find the coordinate points of the image with the given pre-image graphically, simply move the points of the pre-image around the plane to reach the image.

Video-Lesson Transcript

Translation is just a slide of a shape.

We can move this entire shape to the right and up. We can move it to the right and down. Or we can go left and down or left and up. Maybe just up, or just down, or just left, or just right.

The way we denote translation is the capital letter $T$ and then two numbers, we’ll call them $h$ and $k$ . One number is the change in $x$ direction which is $h$ and the other number is the change in $y$ direction which is the $k$ .

If we have $x$ and $y$ coordinates, we’ll just have to add whatever is the value of $h$ and $k$ .

$x + h, y + k$

For example, we have

$T_{(5, -3)}$

This means we’re moving to the right by $5$ because we’re adding $5$ to the $x$ values. Then move down by $3$ since we’re going to add $-3$ to the $y$ values.