In this video, you will learn how to calculate the volume and surface area of select solid figures such as a prism, sphere, cone, cylinder, and pyramid.

The volume of a three-dimensional figure is the amount of space it takes up.
The lateral area of a three-dimensional figure is the sum of the outermost layers of a figure except for the bases.
The surface area of a three-dimensional figure is the sum of the outermost layers of the figure.

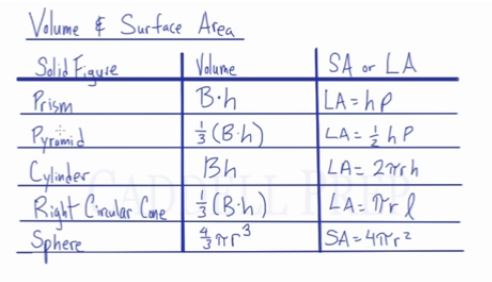
Prism
Volume: $Bh$
Lateral Area: $Ph$
Surface Area: $LA+2B$

Pyramid
Volume: $\frac{1}{3}(Bh)$
Lateral Area: $\frac{1}{2}Pl$
Surface Area: $LA+B$

Cylinder
Volume: $Bh$
Lateral Area: $2\pi rh$
Surface Area: $LA+2B$

Right Circular Cone
Volume: $\frac{1}{3}(Bh)$
Lateral Area: $\pi rl$
Surface Area: $LA+B$

Sphere
Volume: $\frac{4}{3}\pi r^3$
Lateral Area: $4\pi r^2$
Surface Area: $4\pi r^2$

Video-Lesson Transcript

In this lesson, we’ll cover formulas for volume and surface area.

We have a solid figure, the formula for the volume, and the formula for surface area or land area

Let’s start with the prism.

A prism could be a rectangular prism, for example. Where the top and bottom are the same and extended vertically. The bottom is a rectangle and the top is also a rectangle. A cube is also a prism. We have a square on all six sides. We could have a triangle prism as well. The top and bottom are a triangle and the vertical lines are extended upwards.

The volume is $B \times h$

$V = B \times h$

where $B$ is the area of the base, we just have to find out what is the area of the base and then we have to multiply it to the height $h$ .

For a cube, we have to find out what is the area of the base square then multiplied by its height.

And for this triangle, we should find the area of the base triangle multiplied by its height.

That’s finding the volume of a prism.

What is the lateral area?

The lateral area is the area of the sides.

The area of the front, back, left, and right sides. We have to find the lateral area all the way around.

To find the lateral area all the way around it, you just have to multiply the height $h$ by the perimeter $P$ .

$LA = hP$

We have to find out the perimeter of the base. To do this, we just have to add up the lengths multiplied by its height.

We have to find the total surface area, we have to find the area of the top and bottom and add that to the total lateral area.

Pyramid

Now, let’s look at the volume and the surface area of a pyramid.

Pyramid has a square base and then it extends to a point above it. It looks something like this.

We have a square or rectangle base and the sides are all triangles.

The volume formula for the pyramid is

$V = \dfrac{1}{3}(B \times h)$

where $B$ is the area of the base, in this case, the base is a square.

So, we have to calculate the area of the square multiplied it by its height.

Height is from the bottom to the highest point which is if you’re inside, it goes straight down and will make a right angle with the base.

To calculate the lateral area of a pyramid:

$LA = \dfrac{1}{2}hP$

P is the perimeter of the base.

In this case, its the square. Just add up all the sides multiply it by its height and do $\dfrac{1}{2}$ of that, you’ll get the lateral area.

Lateral area is the area of the sides. It excludes the area of the base. That’s why we have to find the area of the square base and add that on.

Cylinder

Now, let’s look at the cylinder.

A cylinder has a circular top and bottom, similar to a can, and has a height.

Volume is

$V = Bh$

much like the prism.

Here, the base is a circle.

We have to find the area of a circle which is $B$ .

Our formula now is

$V = \pi r^{2} h$

The lateral area

$LA = 2 \pi r h$

Here, $2\pi r$ is the formula for circumference.

We have the distance of the circle base multiplied by its height.

Compared to prism’s formula where height multiplied by the perimeter, here, we have height multiplied by circumference.

Lateral area is the area going around the cylinder. But it doesn’t include the top and the bottom. If we had to find the total surface area of a cylinder, we have to calculate the area of the top and the bottom and then add that on as well.

So, the total surface area in this case is

$SA = 2\pi rh + 2\pi r^{2}$

including the top and the bottom.

The total lateral area is just going around the sides.

Right Circular Cone

Now, let’s go over the right circular cone.

The base of a right circular cone is a circle. Then it goes up to a point or an apex.

The volume is

$V = \dfrac{1}{3} Bh$

where $B$ is the area of the base and $h$ is the height computed from the very top to the bottom.

The base is a circle so $B$ is $\pi r^{2}$

Our formula for volume is now

$V = \dfrac{1}{3} \pi r^{2} h$

Now, let’s look at lateral area.

Lateral area is

$LA = \pi r \ell$

where $\ell$ is the length of the side of a cone.

This is a right circular cone so if we drew the height down the middle and extend the radius to that point, we’ll have a right angle.

So, we’ll have a right triangle with the height and radius.

Now that we have a right triangle, we can solve for the length if it’s not given using the Pythagorean theorem.

We do $r^2 + h^2 = \ell^2$ .

The lateral area will give us the area going around the cone but will not include the bottom of the cone.

If we want the total surface area, including the base circle, we have to do the lateral area plus area of the base circle.

$SA = \pi r\ell + \pi r^2$

Sphere

Let’s go over the volume and surface area of a sphere.

A sphere is like a ball or marble. It’s a circular 3D shape.

Volume of a sphere is

$V = \dfrac{4}{3}\pi r^{3}$

and the surface area is

$SA = 4\pi r^2$

The radius go from the center to the edge.

You could think of the surface area if you’re making a leather basketball. You can use the surface area to determine how much leather you would need to make the ball. What amount of area you will need to make a ball.

The nice thing about the near stage amateur regions is that you’re given formulas. You’re not expected to memorize every formula on this list.

They actually give you the formula for the volume of the pyramid but not the formula for lateral area.

Also, they give you the formula for the volume and lateral area of a cylinder.

They give you the formula for the volume and lateral area of a right circular cone.

Furthermore, they also give the formula for the volume and surface area of a sphere.

But remember, when you’re solving for the lateral area in a cylinder and right circular cone is no problem.

But if asked for the surface area, you have to do the lateral area plus the area of the base.

For a cylinder, there’s a base at the top and the bottom.

$SA = LA + B(2)$

So, you have to multiply the base by two.

For the right circular cone,

$SA = LA + B$

it has just one base.