Arcs Formed by Tangents & Secants Which Intersect at an External Point

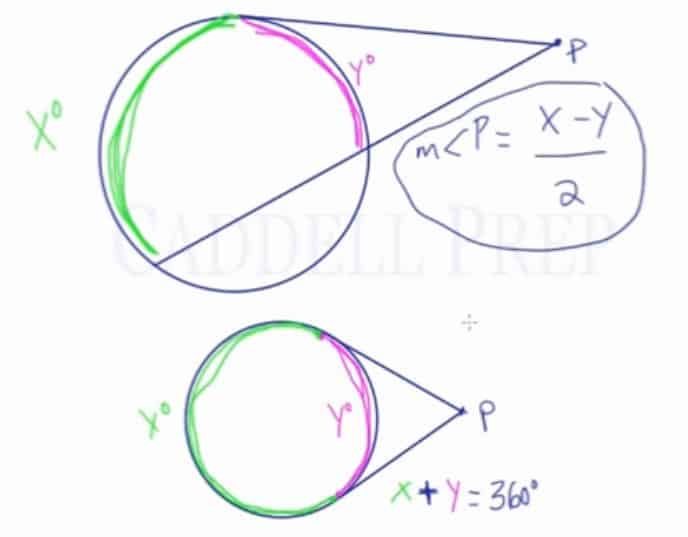
In this video, we are going to look at arcs formed by tangents and/or secants which intersect at an external point.

Given a circle and external point $P$ , let’s draw two secants coming from $P$ . These two lines intersect the circle and form two arcs. Let’s label the larger arc $x$ and the smaller arc $y$ .
$m\angle{P}=\frac{x-y}{2}$

If the measure of the arcs were 100 and 40, then we can find the measure of angle $P$ by doing:
$m\angle{P}=\frac{100-40}{2}=\frac{60}{2}=30$

If the large arc was 100, angle $P$ was 20, and the smaller arc was missing then we can find the smaller arc by:
$20=\frac{100-y}{2}$
$40=100-y$
$-60=-y$
$60=y$

Another variation of this type of question would include a secant line and a tangent line from point $P$ . We still have a larger arc and a smaller arc, labeled as $x$ and $y$ . We still use the same formula to solve for missing values. The only difference is that now we don’t have a missing arc near the top of the circle.

The last variation would have two tangent lines from point $P$ . We still have a larger arc and a smaller arc, labeled as $x$ and $y$ . We still use the same formula to solve for missing values. The only difference is that now we don’t have any missing arcs. This means that the two arcs, $x$ and $y$ , added together would equal 360 since they cover the entirety of the circle.

Video-Lesson Transcript

Let’s take a look at intercepted arcs formed by tangents and secants which intersect at an external point.

We have a circle and an external point $P$ .

Let’s draw two secant lines coming from $P$ .

These two tangent lines intercept the circle and form two arcs. One arc is $x^{\circ}$ and another arc intercepted is $y^{\circ}$ .
And we have angle $P$ . The measure of angle $P$ is

$m\angle P = \dfrac{x - y}{2}$

The measure of large arc minus small arc divided by two will give us the measurement of the angle.

For example,

$x = 100^{\circ}$

$y = 40^{\circ}$

We can find the measure of angle $P$ simply by doing:

$m\angle P = \dfrac{100 - 40}{2}$

$m\angle P = \dfrac{60}{2}$

$m\angle P = 30$

Let’s look at another example.

The measure of the large arc is $100^{\circ}$ , the measure of the small arc is missing, and angle $P$ is $20^{\circ}$ .

Using the formula:

$m\angle P = \dfrac{x - y}{2}$

$20 = \dfrac{100 - y}{2}$

$20 \times 2= \dfrac{100 - y}{2} \times 2$

$40 = 100 - y$

$40 - 100 = 100 - 100 - y$

$-60 = - y$

$\dfrac{-60}{-1} = \dfrac{-y}{-1}$

$60 = y$

So, the measure of the small arc is $60^{\circ}$ .

This is another variation of this type of question involving two types of secants. Except in this variation we have a tangent in the secant.

From point $P$ , we’ll draw a tangent line, not a secant. Then draw a second line which is a secant.

Still, we have a large arc which is $x^{\circ}$ and a smaller arc which is $y^{\circ}$ .

Same exact set-up. Same formula. Except now, we don’t have a missing arc in between.

One arc goes all the way to the point of the tangent line. And the other arc starts at that spot and goes all the way down.

We still have the same formula.

$m\angle P = \dfrac{x - y}{2}$

And the last variation is when we have a circle and an external point $P$ .

Here, we have two tangent lines.

The large arc starts at the top and goes all way around up to this point which we’ll call arc $x^{\circ}$ . And the smaller arc picks up at one tangent point and goes to the other tangent point which we’ll call $y^{\circ}$ .

And we still have the same formula.

$m\angle P = \dfrac{x - y}{2}$

Something you’ll notice on this diagram is if you follow $x$ all the way around into $y$ and back, you’ll see that they are connected.

They actually create a full circle.

This means that arc $x$ plus arc $y$ is going to add up to $360^{\circ}$ .

$x + y = 360^{\circ}$