Tangent Learn About Tangent And Secant Lines

In this video, we are going to look at tangent and secant lines.

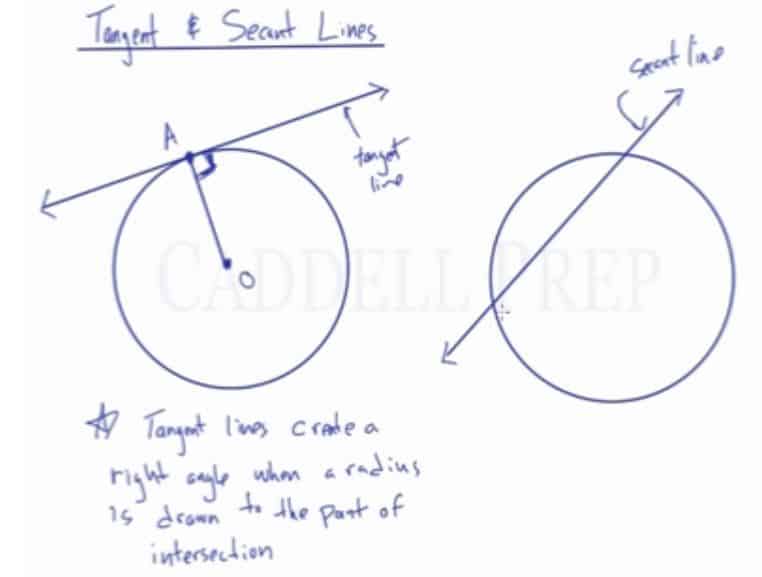
Tangent Line: Line that intersects the circle, but only at one spot.

Secant Line: Line that intersects the circle, but in two spots and continues through the circle.

If the center of the circle is the point $O$ , and the point where the tangent touches the circle is the point $A$ , then $\overline{OA}$ is the radius. The angle that the radius forms with the tangent line is always a right angle.

Video-Lesson Transcript

In this lesson, we’ll take a look at tangent and secant lines.

A tangent line is a line that intersects with a circle in only one spot.

This line drawn intersects with a circle at only one point. So, this is a tangent line.

A secant, on the other hand, intersects in two spots.

This is an example of a secant line.

Remember, a chord also intersects in two spots. But a secant continues through.

The part of a secant inside the circle is a chord. But the entire line is a secant. It extends on both sides and out of the circle.

Something important about the tangent line has to do with the radius.

If we have a point in the middle of the circle called $O$ and the point where the tangent line intersects with the circle is called $A$ . Then, $\overline{\rm OA}$ will be the radius.

The angle that this radius makes with the tangent line is always a $90^{\circ}$ angle.

Very important note:

Tangent lines create a right angle when a radius is drawn to the point of intersection.

Tangent line intersects in one spot while secant intersects in two spots.