Learn About Rotation In The X-Y Plane

In this video, you will learn how to do a rotation graphically and numerically, using the coordinates.

Rotations notations are commonly expressed as
R₉₀, R₁₈₀, and R₂₇₀, where the rotation is always counterclockwise.

Rotations in the clockwise direction corresponds to rotations in the counterclockwise direction:
R_-90 = R₂₇₀,
R_-180 = R₁₈₀,
and R_-270 = R₉₀

Rotation Notations:
R₉₀ (x,y) = (-y,x),
R₁₈₀ (x,y) = (-x,-y),
and R₂₇₀ (x,y) = (y,-x),

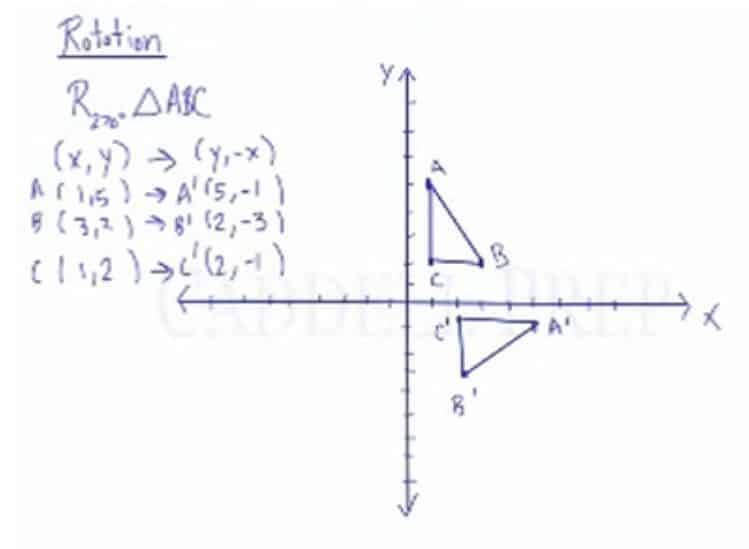
Apply a rotation of 270 degrees to triangle ABC with points A(1,5), B(3,2), and C(1,2).

Identify the appropriate rotation notation
R₂₇₀ (x,y) = (y,-x),

Perform the operation within the notation to each coordinate point
A(1,5) $\rightarrow$ A'(-5,1)
B(3,2) $\rightarrow$ B'(-2,3)
C(1,2) $\rightarrow$ C'(-2,1)

Now, we have the points of the image after the transformation:
A'(-5,1), B'(-2,3), and C'(-2,1)

Video-Lesson Transcript

Let’s talk about rotation on the $xy$ coordinate plane.

We’ll cover rotations of $90^{\circ}$ , $180^{\circ}$ , and $270^{\circ}$ .

First of all, whenever we say rotation of a positive angle, it always means counterclockwise. The hands of a clock move this way, counterclockwise means opposite of the clock. So, counterclockwise is the other direction.

The $x$ -axis and $y$ -axis is perpendicular to each other. That means the angle between them is $90^{\circ}$ .

Rotation of $90^{\circ}$ , we move this triangle from this quadrant or area into the next quadrant.

Rotation of $180^{\circ}$ is going into two quadrants.

$270^{\circ}$ will go into three quadrants.

And we don’t do $360^{\circ}$ because it’s right back where we started. So, don’t worry about rotating $360^{\circ}$ because we’ll end exactly where we started.

You might also see rotations for $-90^{\circ}$ , rotations of $-180^{\circ}$ , and rotations of $-270^{\circ}$ .

If $90^{\circ}$ is counterclockwise, then $-90^{\circ}$ is clockwise direction.

$-90^{\circ}$ is the same as $270^{\circ}$ .

$-180^{\circ}$ is the same as $180^{\circ}$ .

And rotating $-270^{\circ}$ is the same as $90^{\circ}$ .

Now that we have an idea of what quadrant we’d end up in, let’s take a look at the specific rules that tells exactly where each coordinate will go.

$R_{90} (x, y) \rightarrow (-y, x)$

$R_{180} (x, y) \rightarrow (-x, -y)$

$R_{270} (x, y) \rightarrow (y, -x)$

Let’s try rotating this triangle $90^{\circ}$ .

$R_{90} \triangle {ABC}$

Let’s first write down what the rule is.

$R_{90} (x, y) \rightarrow (-y, x)$

$A (1, 5) \rightarrow A^\prime (-5, 1)$

$B (3, 2) \rightarrow B^\prime (-2, 3)$

$C (1, 2) \rightarrow C^\prime (-2, 1)$

What happened is that the $x$ coordinate of $A$ became the $y$ coordinate of $A^\prime$ and the $y$ coordinate became the $x$ coordinate after we negated it.