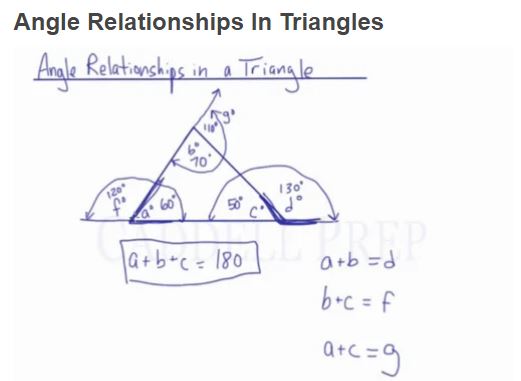
Angle Relationships In Triangles

In this video, we are going to look at the angle relationships in a triangle.

Let’s label the angles a\textdegree, b\textdegree, and c\textdegree. The most common rule for angles in a triangle is:
a\textdegree + b\textdegree + c\textdegree = 180\textdegree

If we extend one side (past angle c as shown in the video) and label it d\textdegree, then there is another rule, which works for all exterior angles.a\textdegree+b\textdegree=d\textdegree

For example:
If a\textdegree=60\textdegree and b\textdegree=70\textdegree, then c\textdegree must be 50\textdegree. Since c=50\textdegree, then d must be 130\textdegree because they lie on a straight line. Therefore, a\textdegree+b\textdegree=d\textdegree.

Angle Relationships In Triangles

Video-Lesson Transcript

In this lesson, we’ll cover angle relationships in a triangle.

A triangle has three angles.

Let’s label them as a^{\circ}, b^{\circ}, and c^{\circ}.

If we add this all up:

a^{\circ} + b^{\circ} + c^{\circ} = 180

If we extend the horizontal line of the triangle going to the right, we will form a new angle. Let’s call this angle d^{\circ}.

a^{\circ} + b^{\circ} = d^{\circ}

Let’s give values to this:

a^{\circ} = 60^{\circ}
b^{\circ} = 70^{\circ}
c^{\circ} = 50^{\circ}

Since c^{\circ} = 50^{\circ}, d^{\circ} should be 130^{\circ} because c and d forms 180^{\circ}

This is also because:

a + b + c = 180
and
c + d = 180

c remains the same in both situations so a + b = d.

This is true for any of these.

If you will extend the horizontal line of the triangle going to the left, let’s label this f^{\circ}.

Then b + c = f

So, if a = 60^{\circ} and a + f = 180, therefore f = 120^{\circ}.

In this case, we proved that b + c = f.

Now, let’s extend the line with angle b and call it angle g^{\circ}.

Since b = 70^{\circ}, the angle beside it is 110^{\circ}.

Therefore, a + c = g

The sum of all the interior angles is equal to 180.

And the exterior angles is equal to the sum of the other two interior angles.