Congruence in Overlapping Triangles

Video-Lesson Transcript

Let’s look at congruence in overlapping triangles.

This can cause a lot of problems to a lot of students.

For example, we have this triangle. And we have something like this. And points A, B, C, D, and E.

We want to prove that
$\triangle ABE \cong \triangle CBD$

This is pretty difficult to see. So, let’s write them using different colors.

One of the steps in proving that these triangles are congruent is we have to find out if certain side and certain angle match up when we’re given certain information. But since we have overlapping triangles, there’s information given in the diagram. That is not given to you as a statement. And we could see it because certain things are congruent because they exist in both of these triangles.

It will make a lot more sense when I show you.

If we look at $\triangle ABE$ , we have an angle $/angle B[\latex]. Then if we look at [latex]\triangle CBD [\latex], we also have that same angle, [latex]\angle B$ .

Because this angle is the same angle in both triangles, it’s congruent to itself.

I’ll just make a small sketch outside. $\triangle ABE$ and $\triangle CBD$ and this angle are the same in both of them.

So, we know that the measure of $m \angle B \cong \angle B$ . Because it is itself.

We know that because of the reflexive property.

Here, the main point is that you have information on congruence based on the diagram.

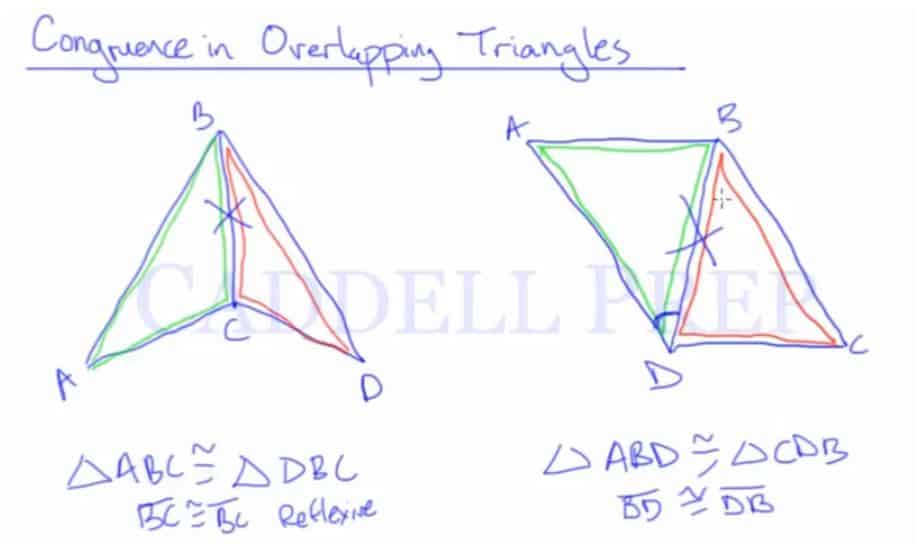
Let’s look at another example.

Here we have a diagram. I want to prove that $\triangle ABC \cong \triangle DBC$ . $\triangle ABC$ is this triangle and $\triangle DBC$ is the other triangle.

Examining this, we should see that they share this side – $\overline{\rm BC}$ .

$\overline{\rm BC} \cong \overline{\rm BC}$ . That is by the reflexive property.

That is the given information just by looking at the diagram. We have one side is congruent to the other side.

One thing I want to point out that confuses a lot of students is that we can’t immediately say that $\angle B$ is congruent to $\angle B$ .

Yes, they both have an angle $\angle B$ . But one angle is separate from the other angle. Just because both are called $\angle B$ doesn’t mean that they are congruent to each other.

$\overline{\rm BC}$ is in both of them. They have both side $\overline{\rm BC}$ and it’s the same exact side. This is how we can use the reflexive property.

Now, let’s take a look at this one.

$\triangle ABD$ and $\triangle CDB$ . I want to prove that these two are congruent.

Again, these both share this side – $\overline{\rm BD}$ . This side is part of one triangle and the same side is part of another triangle. So, we know that it’s congruent to itself.

$\overline{\rm BD} \cong \overline{\rm DB}$

This way, everything is aligned correctly. Because $\angle B$ in one triangle will eventually match up with $\angle D$ in the other triangle. Just by looking at how it’s arranged. $\angle B$ is second and then $\angle D$ is second.

Likewise, $\angle D$ in one triangle will eventually be proven congruent with $\angle B$ in the other triangle. Because they are last.

So, when we name the side, we should name it that they correspond.

But the main point is this side is congruent to itself. Again, we’re given a side based on a diagram.

This is a little bit more advanced. But we can use the reflexive property here also.

Here, we’re trying to prove that $\triangle ABC$ is congruent to $\triangle EDF$ . Let’s say we were given another piece of information.

$\overline{\rm AF} \cong \overline{\rm EC}$

This part is congruent to the other part. These line segments are congruent. But these aren’t a side of a triangle. It’s just part of a side. So, we don’t have a side is congruent to a side at this point.

But if we look at $\overline{\rm AF}$ , it’s a part of the entire side $\overline{\rm AC}$ . $\overline{\rm EC}$ is part of the entire side $\overline{\rm FE}$ .

We don’t have a full side is congruent to a full side of a triangle. But we definitely have a part of a side of the triangle.

If you look at what’s missing from this triangle, you’ll see that $\overline{\rm FC}$ is missing.

If you look at the other triangle, you’ll see that $\overline{\rm CF}$ is missing.

Well, $\overline{\rm FC}$ is the same as $\overline{\rm CF}$ . Then it’s congruent to itself.

In the future, we’ll learn about the addition postulate and substitution. But conceptually, we can make sense of it now.

If $\overline{\rm FC}$ is the same as $\overline{\rm CF}$ , then we would know that $\overline{\rm AC}$ is the same length as $\overline{\rm EF}$ .

I’ll demonstrate it with numbers.

If $\overline{\rm AF}$ is $3$ inches, $\overline{\rm EC}$ is $3$ inches, and $\overline{\rm FC}$ is $6$ inches. Then we know that the length of $\overline{\rm AC}$ is $9$ inches and the length of $\overline{\rm EF}$ is also $9$ inches.

So, we know that $\overline{\rm AC} \cong \overline{\rm EF}$ .

And it’s going to work in any number. No matter what numbers these are, it’s going to be congruent.

$\overline{\rm CF}$ is going to be the same as $\overline{\rm FC}$

So, it’s going to add up to be the same. The total of $\overline{\rm AC}$ is always going to be the same as $\overline{\rm EF}$ .

This is just something to look out for overlapping triangles.