Properties Of Parallelograms

Learn about the properties of parallelograms including relationships among opposite sides, opposite angles, adjacent angles, diagonals and angles formed by diagonals.

Parallelogram Properties

Basic Properties of Parallelograms

Parallelogram: A quadrilateral with two pairs of parallel lines.

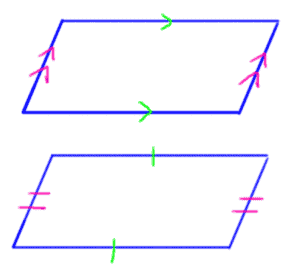
To start off with basic rules, opposite sides of a parallelogram are always equal length and parallel.

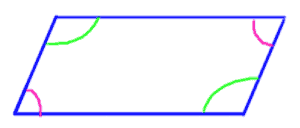
Inside a parallelogram, opposite angles are always congruent. Angles that lie next to each other are always supplementary (add up to 180 degrees).

Diagonals in Parallelograms

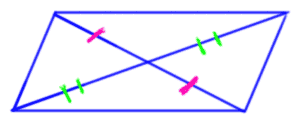
The diagonals in a parallelogram bisect each other.

When the diagonals are drawn, this creates many angles that follow the same rules as do the angles formed by two parallel lines intersected by a transversal. A diagonal acts as a transversal and creates alternate interior angles with the parallel sides.

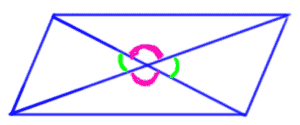
When both diagonals are drawn, two pairs of congruent vertical angles are formed.

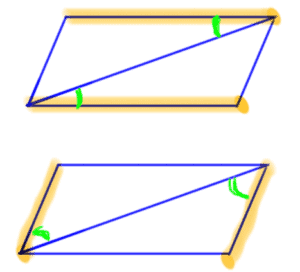
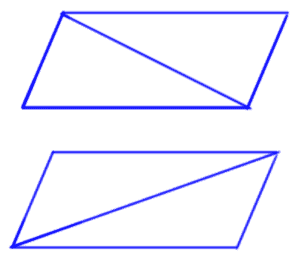
When one diagonal is drawn in a parallelogram, two congruent triangles are formed.

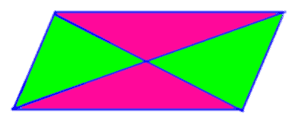
When two diagonals are drawn in a parallelogram, two pairs of congruent triangles are formed.

Special Parallelograms

Rectangles, rhombuses and squares are special types of parallelograms. Therefore, the same rules for angles, sides and diagonals are true for squares and rectangles also. However, these three shapes have additional properties that make them special.

Properties Of Parallelograms

Video-Lesson Transcript

Let’s go over parallelograms.

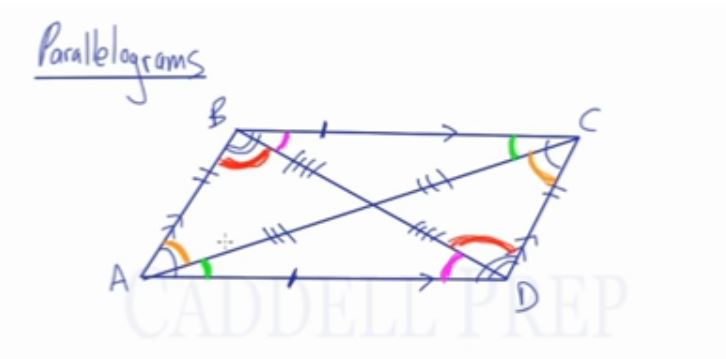
We already drew parallelogram ABCD.

It’s called a parallelogram because there are two pairs of parallel sides.

Side BC is parallel to side AD. And side AB is parallel to side CD.

Besides these two pairs of sides being parallel, they are also congruent.

\overline{\rm BC} \cong \overline{\rm AD}
\overline{\rm AB} \cong \overline{\rm CD}

Angles across from each other are congruent.

m\angle A \cong m\angle C
m\angle B \cong m\angle D

The other way to pair the angles is to make them supplementary.

Angles that are adjacent or next to each other add up to 180.

m\angle A + m\angle D = 180
m\angle A + m\angle B = 180
m\angle C + m\angle B = 180
m\angle C + m\angle D = 180

Angles across from each other are congruent. And if they are next to eaach other, they add up to 180.

Let’s see what happens when we draw diagonals.

Let’s draw a diagonal from A to C and from B to D.

Diagonals actually bisect each other.

BD splits AC in half.

Likewise, AC splits BD in half.

Something else that happens when we draw this diagonal is it affects the angles.

Let me extend this diagonal line and these lines.

Let’s look at these red lines. We’ll see that there are parallel lines and they are intersected by a transversal.

And we know that there is a relationship that happens with the angles.

Because we have a lot of parallel lines intersected by a transversal.

These are all ultimate interior angles.