Proving Triangles are Congruent with ASA or AAS

Video-Lesson Transcript

Let’s go over the angle-side-angle and angle-angle side. Two methods we can use to prove that two triangles are congruent.

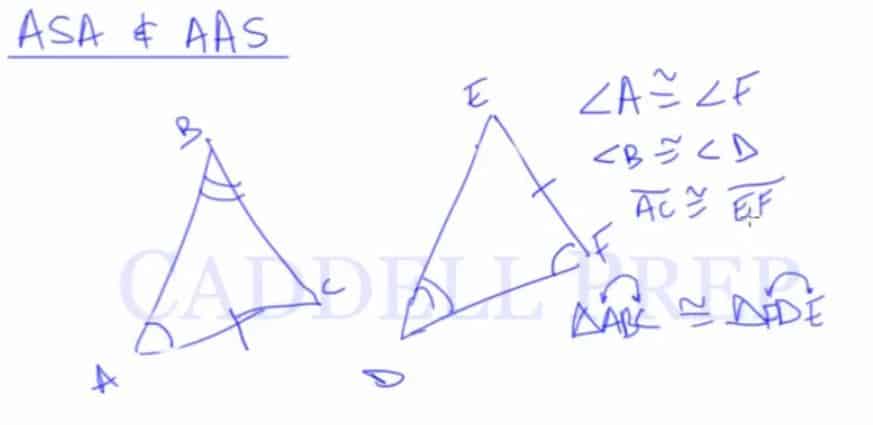
Angle-side-angle (ASA) means we’ll have a side in between two angles.

Here, we have $\angle A \cong \angle E$ and we’re also given $\angle B \cong \angle F$ .

If we are going to use angle-side-angle, we need the side that’s between two angles.

Side $\overline{\rm AB}$ is between the two angles. And if we look at the other triangle, side \overline{\rm EF}.

So, we need to know that $\overline{\rm AB} \cong \overline{\rm EF}$ .

That’s enough to prove that the two triangles are congruent. So, $\triangle ABC \cong \triangle EFD$ .

We just need to label it correctly. Everything that we know is congruent should match up. Everything should be in the same position.

Angle-side-angle is very important that one side is between two angles.

Let’s now use angle-angle-side. We should look at this in order.

We have $\angle A \cong \angle F$ and $\angle B \cong \angle D$ .

Because it’s angle-angle-side, we should have $\overline{\rm BC} \cong \overline{\rm DE}$ .

I just want to point out that if we did have $\overline{\rm BC} \cong \overline{\rm EF}$ , that’s not angle-angle-side. Because the order matters.

Following the direction, we need to have the same side in the same order.

What we would need is $\overline{\rm BC} \cong \overline{\rm DE}$ . Then that’s congruent.

Or we can have it the other way.

$\overline{\rm AC} \cong \overline{\rm FE}$

$\angle A \cong \angle F$

$\angle B \cong \angle D$

$\overline{\rm AC} \cong \overline{\rm EF}$

$\triangle ABC \cong \triangle FDE$

We just have to make sure we write it down correctly. Again, everything we know are congruent should match up.

The first and last point can interchange. But it doesn’t matter.

The way you write it in congruence statement matters.