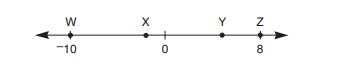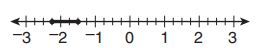63. The set of possible values of is
. What is the set of possible values of
if
?
A.
B.
C.
D.
64.
E.
F.
G.
H.
65. In a certain school, course grades range from to
. Adrianna took
courses and her mean course grade was
. Roberto took
courses. If both students have the same sum of course grades, what was Roberto’s mean?
A.
B.
C.
D.
66. Jenny starts a game with twice as many marbles as Keiko. Jenny gives Keiko marbles, but she still has
more than Keiko. How many marbles did Jenny have to start with?
E.
F.
G.
H.
67. In a scale diagram, inch represents
feet. How many inches represent
foot?
A.
B.
C.
D.
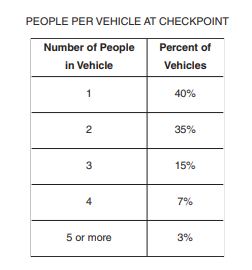
68.
A researcher recorded the number of people in each vehicle that passed through a checkpoint. The table above shows the percent distribution for the vehicles that passed through the checkpoint yesterday morning. How many of the
vehicles contained at least
people?
E.
F.
G.
H.
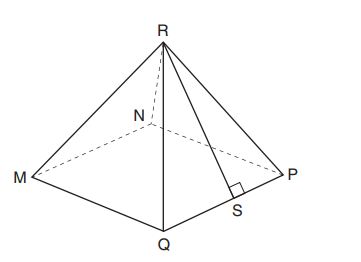
69.
In the pyramid above, each triangular face has the same area, and the base is a square that measures centimeters on each side. If the length of
centimeters, what is the surface area of the pyramid excluding the base?
A. sq cm
B. sq cm
C. sq cm
D. sq cm
70. The perimeter of a rectangle is centimeters. The ratio of the length to the width is
. What are the dimensions of this rectangle?
E. cm by
cm
F. cm by
cm
G. cm by
cm
H. cm by
cm
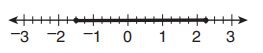
71. Which number line below shows the solution to the inequality ?
A.
B.
C.
D.
72. dollar
lorgs
dollar
dalt
Kevin has lorgs and
dalts. If he exchanges the lorgs and dalts for dollars according to the rates above, how many dollars will he receive?
E.
F.
G.
H.
73. A box of colored pencils contains exactly red pencils. The probability of choosing a red pencil from the box is
. How many of the pencils in the box are not red?
A.
B.
C.
D.
74. The sum of the numbers and
is
. The ratio of
to
is
, and the ratio of
to
is
. What is the value of
?
E.
F.
G.
H.
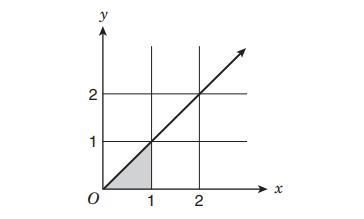
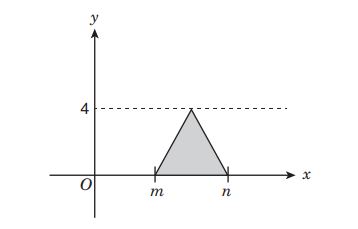
75.
What is the area of the shaded region in the graph above?
A. square unit
B. square unit
C. square unit
D. square unit
76. In Centerville, of the population is female, and
of the population commutes to work daily. Of the total Centerville population,
are females who commute to work daily. What percentage of the total Centerville population are males who do not commute to work daily?
E.
F.
G.
H.
77. Mrs. Cranston bought five bottles of water for each and
pounds of meat. She paid a total of
for these items, not including tax. What was the price per pound of the meat?
A.
B.
C.
D.
78. In a sample of cards,
are red and
are blue. If
cards are selected at random from the sample, one at a time without replacement, what is the probability that both cards are not blue?
E.
F.
G.
H.
79. sind
lorgs
plunks
dalts
sinds
harps
plunk
harps
A nation has five types of coins: sinds, dalts, lorgs, harps, and plunks. The relationship between the coins is shown above. Which coin is most valuable?
A. sind
B. dalt
C. harp
D. plunk
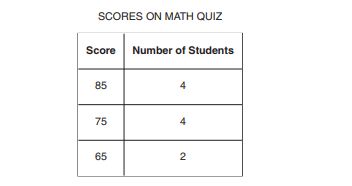
80.
What is the mean score of the students in the table above?
E.
F.
G.
H.
81.
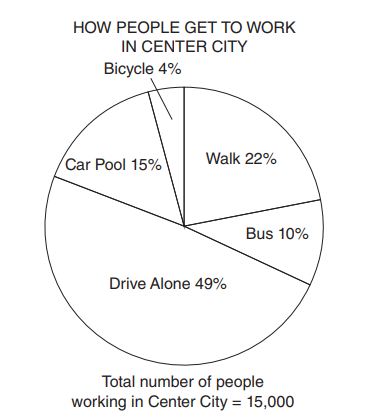
How many more people in Center City walk to work than ride their bicycle to work?
A.
B.
C.
D.
82. Which of the following numbers has factors that include the smallest factor (other than ) of
?
E.
F.
G.
H.
83. In a scale drawing of a triangular banner, one side measures centimeters and the other two sides each measure
centimeters. On the actual banner, these two sides each measure
feet. What is the length of the remaining side of the actual banner?
A. ft
B. ft
C. ft
D. ft
84. The faculty of a certain four-year college consists of teachers. There are
first-year students. The student-to-faculty ratio for the entire college is
to
. What is the total number of second-, third-, and fourth-year students?
E.
F.
G.
H.
85.
What is the value of the expression shown above?
A.
B.
C.
D.
86. A car is traveling miles per hour, and
mile
feet. Which of the following calculations would give the car’s speed in feet per second?
E.
F.
G.
H.
87. Today, Tien’s age is of Jordan’s age. In
years, Tien’s age will be
of Jordan’s age. How old is Jordan today?
A. years old
B. years old
C. years old
D. years old
88. How many positive even factors of are greater than
and less than
?
E.
F.
G.
H.
89. The least of consecutive integers is
, and the greatest is
. What is the value of
in terms of
?
A.
B.
C.
D.
90. Johan leased a car for three years. He paid a one-time fee of , and an additional
per month for the full three years. At the end of the three years, what is the total amount Johan paid for leasing this car?
E.
F.
G.
H.
91. There are different cookies on a plate. Aiden will choose
of these cookies to pack in his lunch. How many different pairs of
cookies can he choose from the
?
A.
B.
C.
D.
92. For a presentation, Deion can create slides in
minutes, working at a constant rate. Kyra can create
slides in
minutes, working at her own constant rate. What is the total number of slides the two of them can create in one hour?
E.
F.
G.
H.
93.
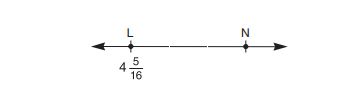
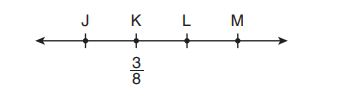
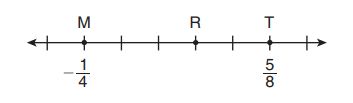
On the number line above, . Point
(not shown) is located between point
and point
. Which value below is a possible value for
?
A.
B.
C.
D.
94. An unmarked straight stick will be laid end over end to measure a distance of exactly feet. The same stick will be used in the same way to measure a distance of exactly
feet. What is the length of the longest possible stick that can be used for both measurements?
E. ft
F. ft
G. ft
H. ft
95. Ryan must read pages for school this weekend. It took him
minutes to read the first
pages. At this rate, how much additional time will it take him to finish the reading?
A. hrs
B. hrs
C. hrs
D. hrs
96. Suppose and
and
do not equal
. What is
in terms of
and
?
E.
F.
G.
H.
97. In the set of consecutive integers from to
, inclusive, there are four integers that are multiples of both
and
. How many integers in this set are multiples of neither
nor
?
A.
B.
C.
D.
98.
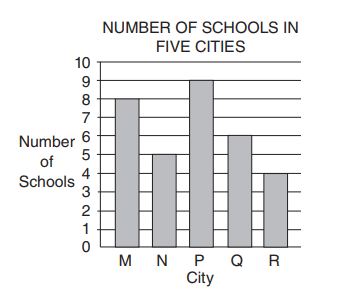
The graph above shows the number of schools per city for five small cities. Cities M and N each have students per school. City P has
students per school. Cities Q and R each have
students per school. Which of the five cities has the greatest number of students?
E. City M
F. City P
G. City Q
H. City R
99. A box contains strawberry candies,
banana candies, and
orange candies. If Braden selects
candies at random from this box, without replacement, what is the probability that both candies are not banana?
A.
B.
C.
D.
100.
In the equation above, and
are positive numbers. Which of these is equal to
?
E.
F.
G.
H.
101.
On the number line above, points and
are integers, and
. What is the value of
?
A.
B.
C.
D.
102. A metal square used in an electronic device must have a thickness of inch, with an allowable error of
percent. What is the greatest allowable thickness of the metal square?
E. in.
F. in.
G. in.
H. in.
103.
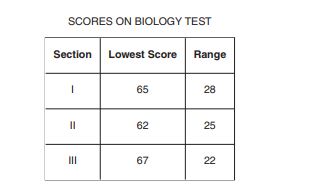
Mr. Blake’s biology class is divided into three sections. The same test was given to each section. The table above shows both the lowest score and the range of scores on this test for each section. What is the overall range of all scores in all three sections?
A.
B.
C.
D.
104. If is a positive even number, how many odd numbers are in the range from
up to and including
?
E.
F.
G.
H.
105.
In the infinitely repeating decimal above, is the first digit in the repeating pattern. What is the
digit?
A.
B.
C.
D.
106. A car travels at feet per minute. The radius of each tire on the car is
foot. How many revolutions does one of these tires make in
minute?
(Use the approximation for
.)
E.
F.
G.
H.
107.
A.
B.
C.
D.
108. A sports store has a container of handballs: blue,
red,
yellow,
white, and
green. If one ball is picked from the container at random, what is the probability that it will be yellow?
E.
F.
G.
H.
109. Each week, Leon has fixed expenses of at his furniture shop. It costs him
to make a chair in his shop, and he sells each chair for
. What is Leon’s profit if he makes and sells
chairs in
week?
A.
B.
C.
D.
110. Using the approximation centimeters
inch, how many centimeters are in
feet
inches?
E.
F.
G.
H.
111.
On the number line above, and
. What is the position of point
?
A.
B.
C.
D.
112. If , what is
in terms of
?
E.
F.
G.
H.
113.
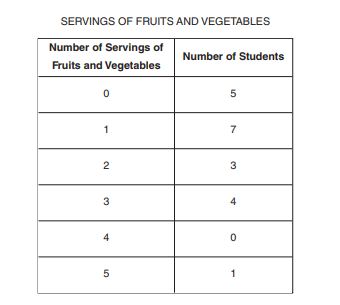
There are students in a class. The frequency table above shows the number of students in this class who ate
or
servings of fruits and vegetables yesterday. What is the mean number of servings of fruits and vegetables eaten yesterday per student in this class?
A.
B.
C.
D.
114. A paste used to cover a billboard is made by mixing the following ingredients by weight: parts powder,
parts water,
parts resin, and
part hardener. To cover one billboard requires
pounds of this paste. How many total pounds of resin are required to cover
billboards?
E.
F.
G.
H.
============================
63. If and
, what is the value of
?
A.
B.
C.
D.
64.
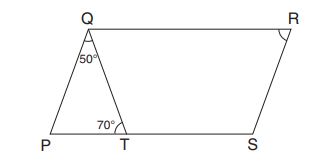
In the figure above, is a parallelogram. The measure of
is
, and the measure of
is
. What is the measure of
?
E.
F.
G.
H.
65.
Based on the statement above, which variable has the greatest value?
A.
B.
C.
D.
66. A roofing contractor uses shingles at a rate of bundles for every
square feet of the roof covered. At this rate, how many bundles of shingles will he need in order to cover a roof that is
square feet?
E.
F.
G.
H.
67. To make party invitations, Macie could buy a package of paper for , or she could buy
individual sheets of the same paper for
each. What is the largest value of
that would make buying the individual sheets less expensive than buying the package?
A.
B.
C.
D.
68. At 1:00 p.m. one day, the temperature was degrees above zero. During the rest of the day, the temperature fell
degrees per hour. What was the temperature at 7:00 p.m. that day?
E.
F.
G.
H.
69. A bag contains marbles that are red, blue, or green. The ratio of red to blue marbles is
, and the ratio of blue to green marbles is
. If
blue marbles are removed and replaced with
green marbles, what will be
the new ratio of red to green marbles?
A.
B.
C.
D.
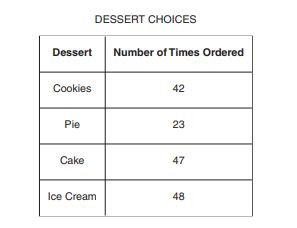
70.
The table above shows the number of times that different desserts were ordered at a restaurant. Based on this information, what is the probability of a customer ordering ice cream as a dessert?
E.
F.
G.
H.
71. What is the least common multiple of and
?
A.
B.
C.
D.
72. One day, the Early Bird Restaurant used dozen eggs for
breakfast customers. At this rate, approximately how many dozen eggs are needed for
breakfast customers?
E.
F.
G.
H.
73. A cooler contains three types of beverages: bottles of apple juice,
bottles of grape juice, and
bottles of orange juice. What is the probability that a bottle chosen at random from this cooler is not apple juice?
A.
B.
C.
D.
74. A large circular dinner plate has a radius of centimeters. A smaller circular plate with a circumference of
centimeters is placed in the center of the larger dinner plate. What is the area of the part of the larger dinner plate that is not covered by the smaller plate?
E. sq cm
F. sq cm
G. sq cm
H. sq cm
75.
The table above shows prices for newspaper advertising. A store purchased pages,
pages, and full-page space in equal numbers for a total of
. What is the total amount of page space the store purchased?
A. pages
B. pages
C. pages
D. pages
76. How many positive odd numbers satisfy the inequality ?
E.
F.
G.
H.
77. If , what is the value of
when
?
A.
B.
C.
D.
78. Points and
are on a straight line, and
is between
and
. Length
, and length
centimeters. What is the length of
?
E. cm
F. cm
G. cm
H. cm
79. Bryana bought yards of cloth at
per yard. If there was an
sales tax, what was the total cost of cloth?
A.
B.
C.
D.
80.
On the number line above, . What is the position of point
?
E.
F.
G.
H.
81. A United States presidential coin is made from an alloy of four metals – copper, zinc, manganese, and nickel – with weights in the ratio of , respectively. The coin weighs a total of
grams. What is the weight of the zinc in this coin?
A. g
B. g
C. g
D. g
82. Jack scored a mean of points per game in his first
basketball games. In his 4th game, he scored
points. What is his mean score for the first 4 games?
E.
F.
G.
H.
83. A cylindrical oil drum can hold liters when it is completely full. Currently, the drum is
full of oil. How many kiloliters of oil need to be added in order to fill the drum completely?
A.
B.
C.
D.
84. Nicole’s age now is three times Carmen’s age. If Carmen will be in two years, how old was Nicole
years ago?
E. yr
F. yr
G. yr
H. yr
85. A chemical decays in such a way that the amount left at the end of each week is less than the amount at the beginning of that same week. What percent of the original amount is left after two weeks?
A.
B.
C.
D.
86. If is an odd integer, which one of the following must be an even integer?
E.
F.
G.
H.
87. Three students stand at the starting line of a running track and begin running laps at the same time. Ann completes lap every
minutes, Jack completes
lap every
minutes, and Lee completes
lap every
minutes. How many laps does Ann complete before all three runners are once again at the starting line at the same time?
A.
B.
C.
D.
88. Simplify this expression:
E.
F.
G.
H.
89.
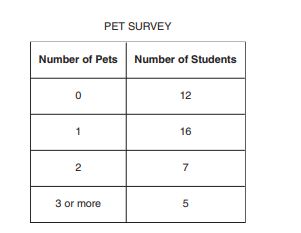
Amy surveyed students at her school about the number of pets they have. What is the probability that a student who participated in the survey has at least pets?
A.
B.
C.
D.
90. A large container is partially filled with liters of water. Ito adds
liters of water to the container, making it
full. If Ignacio adds
more liters of water, the container will be
full. What is the value of
?
E.
F.
G.
H.
91.
If , what is the value of the expression above?
A.
B.
C.
D.
92.
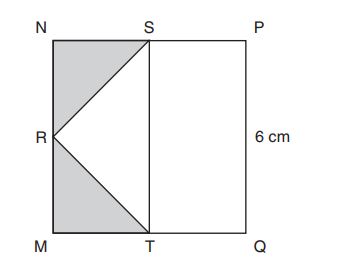
and
are midpoints of the sides of square
, as shown above. What is the sum of the areas of the shaded triangles?
E. sq cm
F. sq cm
G. sq cm
H. sq cm
93. The Chens spend of every
they earn on planned expenses. If the family earns
in one year, how much will they spend on planned expenses that year?
A.
B.
C.
D.
94. A pizza shop offers a choice of sizes (small, medium, and large) and
different toppings. Different pizzas can be created by changing the size and/or the choice of toppings. If Cody wants to order a pizza with exactly
different toppings, how many different pizzas can he create?
E.
F.
G.
H.
95.
The table above shows the number of cats per family in households in the Blaine neighborhood. By what percentage is the number of families with
cat greater than the number of families with
cats?
A.
B.
C.
D.
96. A wooden box has a square base. The height of this box is times the length of one side of the base. If one side of the base is
feet long, what is the volume of this box?
E. cu ft
F. cu ft
G. cu ft
H. cu ft
97. On a bike trip, Rajiv traveled kilometers in
hours, while Shaina traveled
kilometers in
hours. How much less was Rajiv’s mean speed, in kilometers per hour (kph), than Shaina’s?
A.
B.
C.
D.
98. Points and
represent
and
, respectively, on a number line. How many units is the midpoint of
from the midpoint of
?
E.
F.
G.
H.
99. There are cubic centimeters in
liter, and
cubic millimeters in
milliliter. How many cubic millimeters are there in
cubic centimeters?
A.
B.
C.
D.
100.
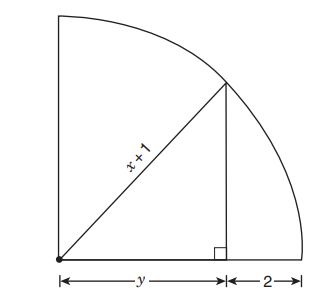
In the quarter circle above, what is in terms of
?
E.
F.
G.
H.
101.
The hash marks on the number line above are evenly spaced. What is the coordinate of point ?
A.
B.
C.
D.
102. Phan chose an Internet service that charges per month plus
per minute. Deion chose an Internet service that charges
per month for unlimited usage. At the end of the month, Phan’s and Deion’s charges were identical. For how many minutes did Phan use the Internet service that month?
E.
F.
G.
H.
103. In a sample of cars at a local dealership, there are
red cars and
cars with backup cameras. Of the
red cars,
have backup cameras. If a car is selected at random from the given sample, what is the probability that both of the following are true: the car is not red and does not have a backup camera?
A.
B.
C.
D.
104. The decimal can be written as the fraction
. What is the value of
?
E.
F.
G.
H.
105.
What is the area of the shaded triangle shown above?
A.
B.
C.
D.
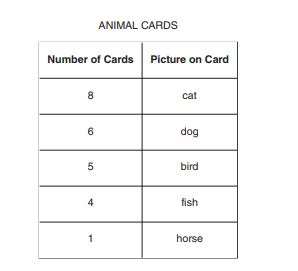
106.
The cards in the table above are mixed in a box. Which animal pictured on a card has exactly a in
chance of being picked at random from the box?
E. cat
F. dog
G. fish
H. horse
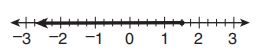
107. Which number line below shows the solution set for when
?
A.
B.
C.
D.
108.
In the equation above, what is the value of ?
E.
F.
G.
H.
109. A ball is selected at random from a box that contains black balls,
green balls, and
red balls. What is the probability that the ball selected is black?
A.
B.
C.
D.
110. At North High School, a survey asked two questions, Question A and Question B. For each question, students could answer either “yes” or “no.” Of the students who responded to the survey,
answered “yes” to Question A, and
answered “yes” to Question B. What is the least possible number of these students who could have answered “yes” to both questions?
E.
F.
G.
H.
111. Raoul is at least years older than Vahn. Which of the following inequalities gives the relationship between Raoul’s age (
) and Vahn’s age (
)?
A.
B.
C.
D.
112. sind
ricks
sind
dalts
Using the conversion above, how many dalts are equal to rick?
E.
F.
G.
H.
113. There are now cans stacked on a shelf that holds
cans when full. If
of these cans were removed, the shelf would be half full. What is the value of
?
A.
B.
C.
D.
114. Carlos tossed a paper cup in the air times and found that the probability of it landing on its side was
. If he tosses the cup in the air
more times, what is the total number of times he can expect the cup to land on its side?
E.
F.
G.
H.
Grade 9 Math
3.
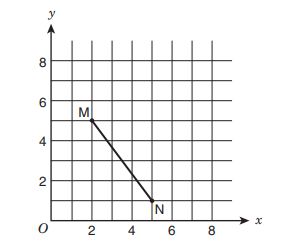
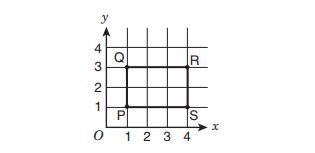
If is translated
unit to the left to produce
, what is the area of parallelogram
?
A. square units
B. square units
C. square units
D. square units
4. Simplify:
E.
F.
G.
H.
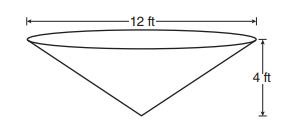
5.
Water is pumped into a tank that is shaped like the right inverted cone shown above. The cone has a base diameter of feet and a height of
feet. What is the volume, in cubic feet, of the water in the tank when the height of the water is
feet?
A. cu ft
B. cu ft
C. cu ft
D. cu ft
6.
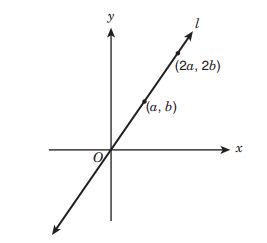
Straight line passes through the origin, as shown in the figure above. What is the slope of line
in terms of
and
?
E.
F.
G.
H.
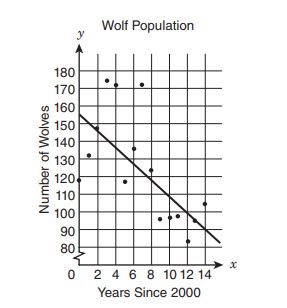
7. The graph shows the wolf population in Yellowstone National Park since 2000. A student drew a line of best fit to model the data.
Which statement best describes the line of fit that the student drew?
A. The line of best fit is not a strong model for the data, because the points are not close to the line.
B. The line of best fit is not a strong model for the data, because it does not pass through any of the data points.
C. The line of best fit is a strong model for the data, because both the line and the data show a negative trend.
D. The line of best fit is a strong model for the data, because about half the data points are on each side of the line.
8. To determine the price of servicing a car, a mechanic charges a fixed fee plus an hourly rate for each hour he works. If his price for hours of service is
, and his price for
hours of work is
, what is the fixed fee that the mechanic charges?
E.
F.
G.
H.
9.
Rectangle above is rotated
about the origin to form rectangle
. What are the coordinates of
?
A.
B.
C.
D.
10.
What is the quotient of the expression above, expressed in scientific notation?
E.
F.
G.
H.
11. Which of the following expressions is negative in value?
A.
B.
C.
D.
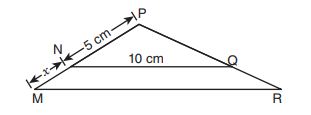
12.
In the figure above, is similar to
. If the length of
is
centimeters, what is the length of
in terms of
?
E.
F.
G.
H.
13. The symbol means
.
What is the value of ?
A.
B.
C.
D.
Additional SHSAT Resources
SHSAT: Everything You Need to Know About the Test
9th Grade SHSAT
SHSAT Score Calculator
SHSAT Prep
Online SHSAT Tutoring
SHSAT 2015-2016
SHSAT 2016-2017