The coin rotation paradox is an intriguing puzzle that has baffled countless individuals for decades. The paradox involves a coin set on a rotating disc, which appears to move impossibly as the disc rotates. Numerous individuals have attempted to solve this paradox, but it remains a mystery to this day. This essay will investigate the coin rotation paradox and discuss potential solutions.
Infamously, the 1982 SAT contained a math question so difficult that not even its creators included a correct answer. The error necessitated rescoring 300,000 examinations, academic victims of a complex coin rotation paradox.
The coin rotation paradox is a classic illustration of how our minds can sometimes deceive us. At first observation, the coin appears to be moving contrary to physical laws. Upon closer examination, it becomes clear that the paradox is merely an optical illusion caused by how our minds process visual information.
So, how does the paradox work? Place two quarters on the table in a level, touching position. Roll the other quarter around the stationary coin while maintaining edge contact and preventing it from sliding. When the moving quarter returns to its initial position, how many complete rotations will it have completed? In other terms, how often has George Washington resumed his standing position? If you enjoy puzzles like this, give it some thought.
Many individuals believe that George will complete one rotation. The circumference of a quarter is about three inches. Therefore, the moving quarter travels along a three-inch-long path, the same distance as its circumference. Indeed, if we coil a string around a quarter and roll it along a three-inch path, unfurling it as we go, three inches of the string will unfurl, just enough for one rotation.
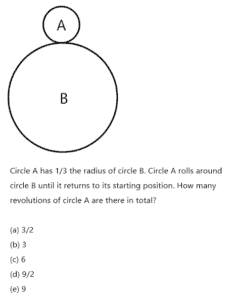
The version of this problem that snuck onto the 1982 SAT math portion featured a minor variation: the disk in the center was more significant than the disk surrounding it. Here is a version of the problem with significantly modified language for clarity:
The larger circle’s radius is stated to be three times that of the smaller circle. This implies that the circumferences of the two circles are identical: B is three times longer than A along its perimeter. It is tempting to conclude that the smaller circle could “unwrap” itself precisely three times to encase the larger circle. Therefore, “3” was the intended SAT multiple-choice response.
In actuality, circle A completes four rotations during its journey, precisely one more than intuition predicts. Even the most astute students were compelled to submit an incorrect answer because the test writers were unaware of the paradox that the number four was not offered as one of the possible answers. The issue was reported to the College Board by three of the 300,000 students who took the exam containing the question, and every exam had to be rescored.
Why, then, is there an additional rotation? The approach that led us astray contains some sageness. Rolling a quarter along a linear path of three inches would require only one rotation. Similarly, a compact circle rolling in a straight line with a length equal to three times its diameter would complete three revolutions. Therefore, the circular geometry of the path induces its own rotation. Imagine rolling a quarter around the perimeter of a tiny poppy seed to comprehend why. George will rotate once despite the negligible distance around the seed. Therefore, there are two rotation sources: rolling along a path, which contributes more rotations the more extended the path, and revolving around an object, which contributes one rotation regardless of size.
Imagine rolling a quarter around a square for another insightful perspective. Each edge of the square is a straight-line segment. George’s head will rotate once for every three inches of length; however, once you reach a corner, the quarter will need to rotate further to clear the corner. This additional rotation at the corners is precisely 90 degrees, resulting in one full rotation (360 degrees) when the coin traverses all four corners of the square and returns to its starting point. Similarly, rolling around a triangle would require a rotation of 120 degrees at each corner.
Simpler Explanation
- If the circumference of a coin is 2 inches, then it will roll completely around on its edge after traveling 2 inches. It will roll completely around twice (complete two rotations) in 4 inches.
- In the question, the small circle has a diameter that is 1/3 of the large circle. Therefore, the small circle has a circumference that is 1/3 of the large circle. (The circumference of the small circle could be 2 inches, and the circumference of the large circle could be 6 inches).
- Just from looking at the lengths of the circumference, the small circle would rotate 3 times from traveling the length of the large circle’s circumference.
- The small circle also naturally makes one rotation because it is traveling in a circular motion around the large circle, instead of rolling on a flat surface.
- The additional rotation doesn’t happen separately from the other rotation. The circle is rotating from rolling along a surface and also rotating from traveling around a circle.
- By the time the circle returns to the original position, it would have rotated four times.
Deeper Analysis
The impact extends to celestial bodies. The moon has a famous far side that always presents the same aspect as Earth. Numerous individuals mistakenly conclude that the moon does not rotate on its axis like the Earth because its appearance does not change. However, if the moon did not rotate during its orbit, we would see its far side from specific locations on Earth. This can be demonstrated by rotating your knuckles around one another in a non-rotating circle. Observers standing on one of your stationary knuckles will see the orbiting fist differently at various times. To conceal its posterior, the moon must rotate once each time it completes an orbit.
This precise parity between orbit time and rotation time is not an astronomical coincidence but rather an instance of tidal locking. With the coins and the SAT problem, we observed two sources of rotation: some from “straight-line” rolling along any path and an additional source from revolving around an object. The moon does not travel in a straight line. If the Earth were flat, the moon would float without rolling above it. Therefore, the moon’s single rotation is due to its revolution around the spherical Earth.
Utilizing a high-speed camera to record the disc’s rotation and the coin’s movement is one possible solution to the coin rotation paradox. By analyzing the video frame by frame, we can determine that the coin is not genuinely moving in a circle but in a series of tangent straight lines to the disc. This phenomenon is commonly observed in physics and is known as rectilinear motion.
Using a mathematical formula to compute the coin’s trajectory is another method for resolving the coin rotation paradox. By considering the speed and direction of the disc’s rotation and the position and velocity of the coin, we can accurately forecast the coin’s movement. This method necessitates a profound understanding of physics and mathematics. Still, it can be a fruitful means to resolve the paradox.
In conclusion, the coin rotation paradox is a fascinating puzzle that has baffled countless individuals. There are numerous ways to approach the paradox and obtain a deeper understanding of the physical and mathematical laws despite the absence of a unique solution. Whether you use a high-speed camera, a mathematical formula, or another method, the most important thing is maintaining an open mind and being willing to investigate new ideas.