Percents And Fractions (Introduction To Percents)

Summary: What does percent mean? Learn what 30% means and how to represent it as a fraction. After you finish this lesson, view all of our Pre-Algebra lessons and practice problems.

Examples of Percents and Fractions

Examples 1

Convert percent 48\% into fraction

48\%=\dfrac{48}{100}

Simplify the fraction

\dfrac{48}{100}=\dfrac{24}{50}=\dfrac{12}{25}

Now, we have:

\dfrac{12}{25}

Examples 2

Convert percent 65\%into fraction

65\%=\dfrac{65}{100}

Simplify the fraction

\dfrac{65}{100}=\dfrac{13}{20}

Now, we have:

\dfrac{13}{20}

Video-Lesson Transcript

In this video, you will learn what percent means and how to represent it as a fraction.

For example, 10\% = \dfrac{10}{100}

Likewise 40\% = \dfrac{40}{100}

And 50\% = \dfrac{50}{100}

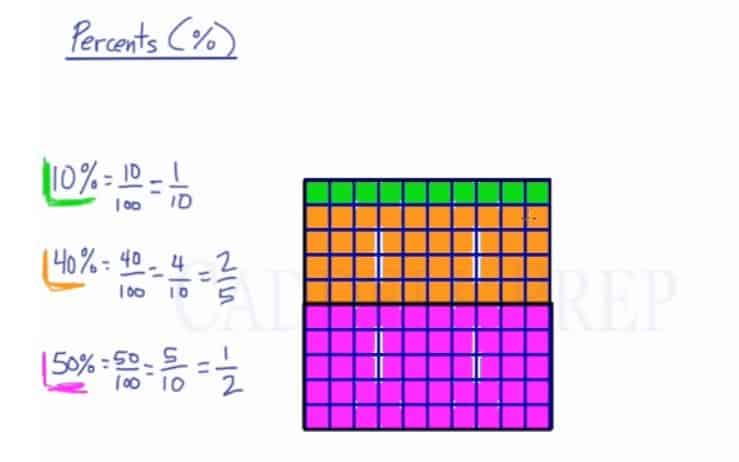
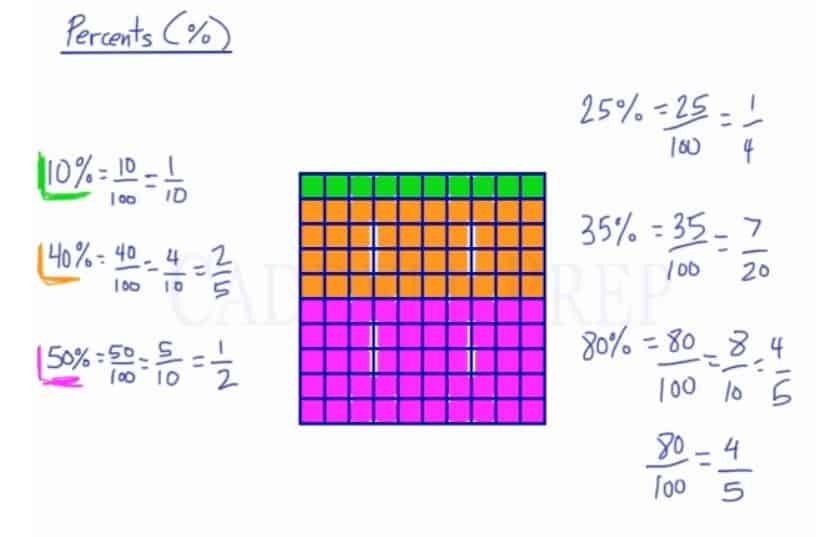
The colored boxes represents the Percentage.

Simplifying the Fraction

At this point, you should probably know how to simplify fractions.

So, let’s do it.

\dfrac{10}{100} = \dfrac{1}{10} \dfrac{40}{100} = \dfrac{4}{10} \dfrac{50}{100} = \dfrac{5}{10}

Then we can re-draw the 100 squares into 10 rectangles.

We can reduce this further, though.

\dfrac{40}{10} = \dfrac{2}{5} \dfrac{5}{10} = \dfrac{1}{2}

So there! We already discussed how to convert percent into fraction.

Percent And Fractions

Review Converting a Fraction to a Decimal and Reducing

Just to review, to convert the percent into a fraction, we have to take the amount in percentage as the numerator and the denominator is always 100. Then reduce it as much as possible.

So if we have 25 \% we could convert it into = \dfrac{25}{100}

Then reduce it and we’ll have \dfrac{1}{4}

If we have 35 \% we could convert it into = \dfrac{35}{100}

And further reduce it into \dfrac{7}{20}

80 \% could be converted into = \dfrac{80}{100}

Then reduce it further to \dfrac{4}{5}

Percent and Fractions 2