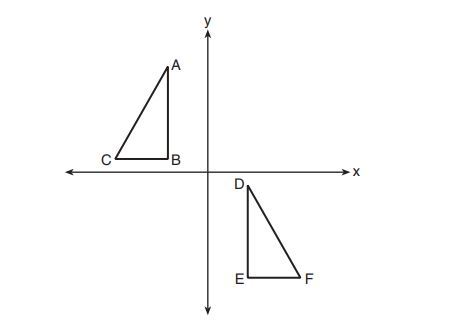
1. In the diagram below, .
Which sequence of transformations maps onto
?
(1) a reflection over the -axis followed by a translation
(2) a reflection over the -axis followed by a translation
(3) a rotation of about the origin followed by a translation
(4) a counterclockwise rotation of about the origin followed by
a translation
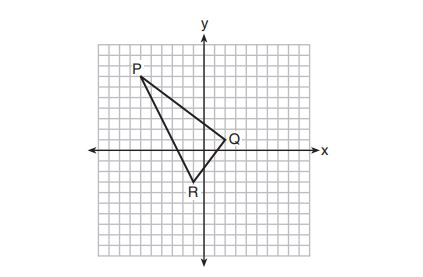
2. On the set of axes below, the vertices of have coordinates
, and
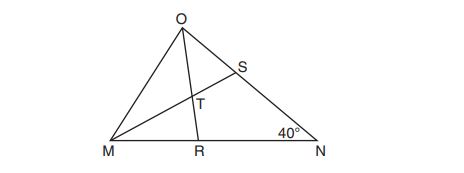
.
What is the area of ?
(1)
(2)
(3)
(4)
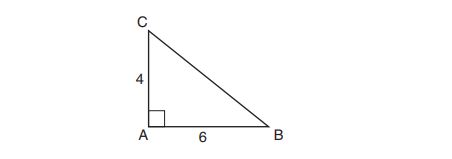
3. In right triangle . If
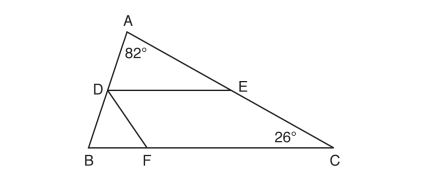
, which function also equals
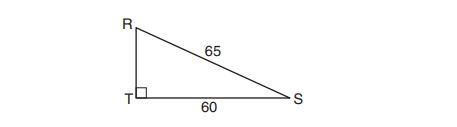
?
(1)
(2)
(3)
(4)
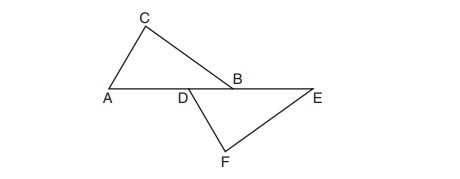
4. In the diagram below, .
What is the number of degrees in the measure of ?
(1)
(2)
(3)
(4)
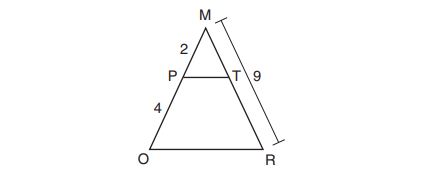
5. Given shown below, with trapezoid
and
.
What is the length of ?
(1)
(2)
(3)
(4)
6. A line segment is dilated by a scale factor of centered at a point not on the line segment. Which statement regarding the relationship between the given line segment and its image is true?
(1) The line segments are perpendicular, and the image is one-half of the length of the given line segment.
(2) The line segments are perpendicular, and the image is twice the length of the given line segment.
(3) The line segments are parallel, and the image is twice the length of the given line segment.
(4) The line segments are parallel, and the image is one-half of the length of the given line segment.
7. Which figure always has exactly four lines of reflection that map the figure onto itself?
(1) square
(2) rectangle
(3) regular octagon
(4) equilateral triangle
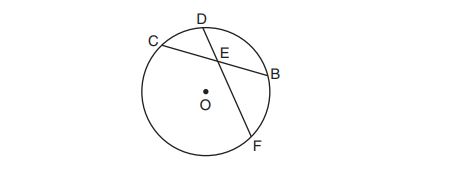
8. In the diagram below of circle , chord
bisects chord
at
.
If and
is
more than
, then
is
(1)
(2)
(3)
(4)
9. Kelly is completing a proof based on the figure below.
She was given that , and has already proven
. Which pair of corresponding parts and triangle congruency method would not prove
?
(1) and SAS
(2) and SAS
(3) and AAS
(4) and ASA
10. In the diagram below, divides
and
proportionally,
and
bisects
.
The measure of angle is
(1)
(2)
(3)
(4)
11. Which set of statements would describe a parallelogram that can always be classified as a rhombus?
I. Diagonals are perpendicular bisectors of each other.
II. Diagonals bisect the angles from which they are drawn.
III. Diagonals form four congruent isosceles right triangles.
(1) I and II
(2) I and III
(3) II and III
(4) I, II, and III
12. The equation of a circle is . What are the
coordinates of the center and the length of the radius of the circle?
(1) center () and radius
(2) center () and radius
(3) center () and radius
(4) center () and radius
13. In the diagram of below,
and
.
What is the measure of , to the nearest degree?
(1)
(2)
(3)
(4)
14. Triangle is the image of
after a dilation followed by a translation.
Which statement(s) would always be true with respect to this sequence of transformations?
I.
II.
III.
IV.
(1) II, only
(2) I and II
(3) II and III
(4) II, III, and IV
15. Line segment has endpoints
and
. Point
is on
such that
is
. What are the coordinates of point
?
(1) ()
(2) ()
(3) ()
(4) ()
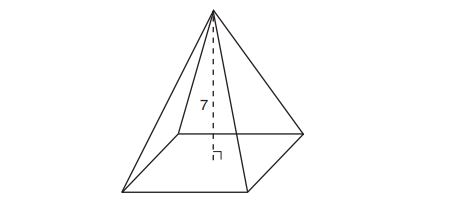
16. The pyramid shown below has a square base, a height of , and a volume of
.
What is the length of the side of the base?
(1)
(2)
(3)
(4)
17. In the diagram below of triangle and
are bisected by
and
, respectively. Segments
and
intersect at
, and
.
If , the measure of angle
is
(1)
(2)
(3)
(4)
18. In the diagram below, right triangle has legs whose lengths are
and
.
What is the volume of the three-dimensional object formed by continuously rotating the right triangle around ?
(1)
(2)
(3)
(4)
19. What is an equation of a line that is perpendicular to the line whose equation is and passes through (
)?
(1)
(2)
(3)
(4)
20. In quadrilateral shown below,
.
Which information would be sufficient to prove quadrilateral is a parallelogram?
(1)
(2)
(3)
(4)
21. A ladder feet long leans against a building, forming an angle of
with the level ground.
To the nearest foot, how high up the wall of the building does the ladder touch the building?
(1)
(2)
(3)
(4)
22. In the two distinct acute triangles and
,
. Triangles
and
are congruent when there is a sequence of rigid motions that maps
(1) onto
, and
onto
(2) onto
, and
onto
(3) onto
, and
onto
(4) point onto point
, and
onto
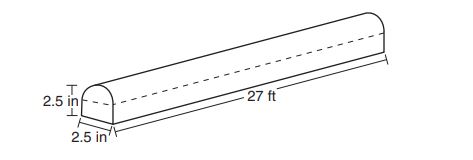
23. A fabricator is hired to make a -foot-long solid metal railing for the stairs at the local library. The railing is modeled by the diagram below. The railing is
inches high and
inches wide and is comprised of a rectangular prism and a half-cylinder.
How much metal, to the nearest cubic inch, will the railing contain?
(1)
(2)
(3)
(4)
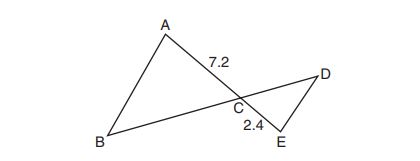
24. In the diagram below, and
.
Which statement is not sufficient to prove ?
(1)
(2) and
(3) and
(4) and