January 2017 Geometry Regents

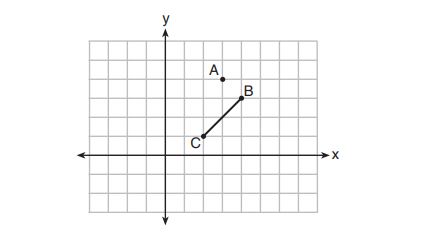
1. Which equation represents the line that passes through the point ( $-2,2$ ) and is parallel to $y = \dfrac{1}{2}X + 8$ ?

(1) $y = \dfrac{1}{2}x$
(2) $y = -2x - 3$
(3) $y = \dfrac{1}{2}x + 3$
(4) $y = -2x + 3$

2. In the diagram below, $\triangle ADE$ is the image of $\triangle ABC$ after a reflection over the line $AC$ followed by a dilation of scale factor $\dfrac{AE}{AC}$ centered at point $A$ .

Which statement must be true?

(1) $m\angle BAC = m\angle AED$
(2) $m\angle ABC = m\angle ADE$
(3) $m\angle DAE = \dfrac{1}{2}m\angle BAC$
(4) $m\angle ACB = \dfrac{1}{2}m\angle DAB$

3. Given $\triangle ABC \cong \triangle DEF$ , which statement is not always true?

(1) $\overline{BD} \cong \overline{DF}$
(2) $m\angle A = m\angle D$
(3) area of $\triangle ABC$ = area of $\triangle DEF$
(4) perimeter of $\triangle ABC$ = perimeter of $\triangle DEF$

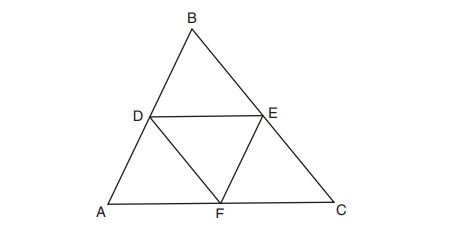
4. In the diagram below, $\overline{DE}, \overline{DF},$ and $\overline{EF}$ are midsegments of $\triangle ABC$ .

The perimeter of quadrilateral $ADEF$ is equivalent to

(1) $AB + BC + AC$
(2) $\dfrac{1}{2}AB + \dfrac{1}{2}AC$
(3) $2AB + 2AC$
(4) $AB + AC$

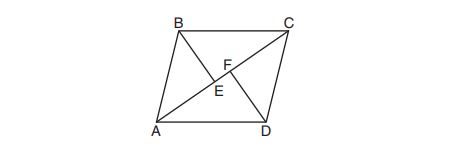
5. In the diagram below, if $\triangle ABE \cong \triangle CDF$ and $\overline{AEFC}$ is drawn, then it could be proven that quadrilateral $ABCD$ is a

(1) square
(2) rhombus
(3) rectangle
(4) parallelogram

6. Under which transformation would $\triangle A'B'C'$ , the image of $\triangle ABC$ , not be congruent to $\triangle ABC$ ?

(1) reflection over the $y$ -axis
(2) rotation of $90^{\circ}$ clockwise about the origin
(3) translation of $3$ units right and $2$ units down
(4) dilation with a scale factor of $2$ centered at the origin

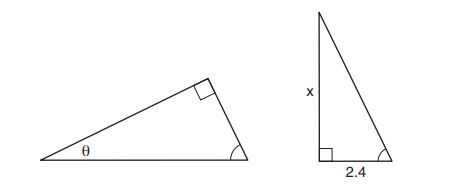
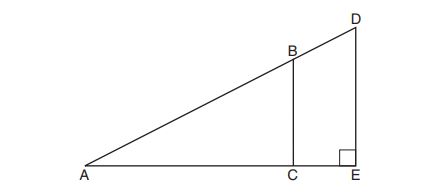
7. The diagram below shows two similar triangles.

If $tan \theta = \dfrac{3}{7}$ , what is the value of $x$ , to the nearest tenth?

(1) $1.2$
(2) $5.6$
(3) $7.6$
(4) $8.8$

8. A farmer has $64$ feet of fence to enclose a rectangular vegetable garden. Which dimensions would result in the biggest area for this garden?

(1) the length and the width are equal
(2) the length is $2$ more than the width
(3) the length is $4$ more than the width
(4) the length is $6$ more than the width

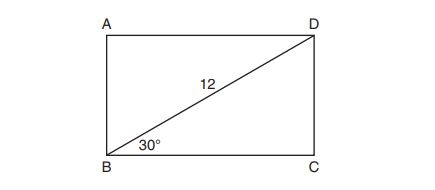
9. The diagram shows rectangle $ABCD$ , with diagonal $\overline{BD}$ .

What is the perimeter of rectangle $ABCD$ , to the nearest tenth?

(1) $28.4$
(2) $32.8$
(3) $48.0$
(4) $62.4$

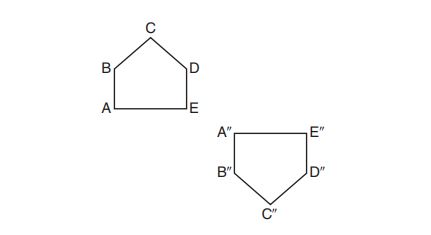
10. Identify which sequence of transformations could map pentagon $ABCDE$ onto pentagon $A''B''C''D''E''$ , as shown below.

(1) dilation followed by a rotation
(2) translation followed by a rotation
(3) line reflection followed by a translation
(4) line reflection followed by a line reflection

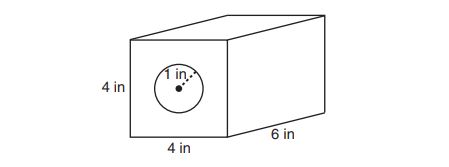
11. A solid metal prism has a rectangular base with sides of $4$ inches and $6$ inches, and a height of $4$ inches. A hole in the shape of a cylinder, with a radius of $1$ inch, is drilled through the entire length of the rectangular prism.

What is the approximate volume of the remaining solid, in cubic inches?

(1) $19$
(2) $77$
(3) $93$
(4) $96$

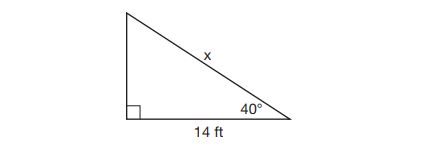
12. Given the right triangle in the diagram below, what is the value of $x$ , to the nearest foot?

(1) $11$
(2) $17$
(3) $18$
(4) $22$

13. On the graph below, point $A(3,4)$ and $\overline{BC}$ with coordinates $B(4,3)$ and $C(2,1)$ are graphed.

What are the coordinates of $B'$ and $C'$ after $\overline{BC}$ undergoes a dilation centered at point $A$ with a scale factor of $2$ ?

(1) $B'(5,2)$ and $C'(1,-2)$
(2) $B'(6,1)$ and $C'(0,-1)$
(3) $B'(5,0)$ and $C'(1,-2)$
(4) $B'(5,2)$ and $C'(3,0)$

14. In the diagram of right triangle $ADE$ below, $\overline{BC} \| \overline{DE}$ .

Which ratio is always equivalent to the sine of $\angle A$ ?

(1) $\dfrac{AD}{DE}$
(2) $\dfrac{AE}{AD}$
(3) $\dfrac{BC}{AB}$
(4) $\dfrac{AB}{AC}$

15. In circle $O$ , secants $\overline{ADB}$ and $\overline{AEC}$ are drawn from external point $A$ such that points $D, B, E,$ and $C$ are on circle $O$ . If $AD = 8, AE = 6$ , and $EC$ is $12$ more than $BD$ , the length of $\overline{BD}$ is

(1) $6$
(2) $22$
(3) $36$
(4) $48$

16. A parallelogram is always a rectangle if

(1) the diagonals are congruent
(2) the diagonals bisect each other
(3) the diagonals intersect at right angles
(4) the opposite angles are congruent

17. Which rotation about its center will carry a regular decagon onto itself?

(1) $54^{\circ}$
(2) $162^{\circ}$
(3) $198^{\circ}$
(4) $252^{\circ}$

18. The equation of a circle is $x^{2} + y^{2} - 6y + 1 = 0$ . What are the
coordinates of the center and the length of the radius of this circle?

(1) center ( $0,3$ ) and radius = $2\sqrt{2}$
(2) center ( $0,-3$ ) and radius = $2\sqrt{2}$
(3) center ( $0,6$ ) and radius = $\sqrt{35}$
(4) center ( $0,-6$ ) and radius = $\sqrt{35}$

19. Parallelogram $ABCD$ has coordinates $A(0,7)$ and $C(2,1)$ . Which statement would prove that $ABCD$ is a rhombus?

(1) The midpoint of $\overline{AC}$ is ( $1,4$ )
(2) The length of $\overline{BD}$ is $\sqrt{40}$
(3) The slope of $\overline{BD}$ is $\dfrac{1}{3}$
(4) The slope of $\overline{AB}$ is $\dfrac{1}{3}$

20. Point $Q$ is on $\overline{MN}$ such that $MQ:QN = 2:3$ . If $M$ has coordinates ( $3,5$ )
and $N$ has coordinates ( $8,5$ ), the coordinates of $Q$ are

(1) ( $5,1$ )
(2) ( $5,0$ )
(3) ( $6,-1$ )
(4) ( $6,0$ )

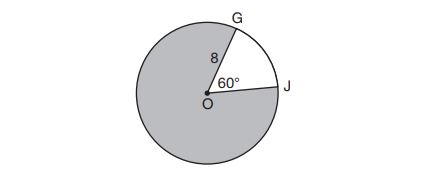
21. In the diagram below of circle $O, GO = 8$ and $m\angle GOJ = 60^{\circ}$ .

What is the area, in terms of $\pi$ , of the shaded region?

(1) $\dfrac{4\pi}{3}$
(2) $\dfrac{20\pi}{3}$
(3) $\dfrac{32\pi}{3}$
(4) $\dfrac{160\pi}{3}$

22. A circle whose center is the origin passes through the point ( $5,12$ ). Which point also lies on this circle?

(1) ( $10,3$ )
(2) ( $-12,13$ )
(3) ( $11,2\sqrt{12}$ )
(4) ( $-8,5\sqrt{21}$ )

23. A plane intersects a hexagonal prism. The plane is perpendicular to the base of the prism. Which two-dimensional figure is the cross
section of the plane intersecting the prism?

(1) triangle
(2) trapezoid
(3) hexagon
(4) rectangle

24. A water cup in the shape of a cone has a height of $4$ inches and a maximum diameter of $3$ inches. What is the volume of the water in the cup, to the nearest tenth of a cubic inch, when the cup is filled to half its height?

(1) $1.2$
(2) $3.5$
(3) $4.7$
(4) $14.1$