SAT Math Lesson 2: Rates, Ratios, Proportions, and Data & Probability

Rates, Ratios & Proportions

What are Rates, Ratios, and Proportions?

An example of a rate is 25 miles/hr, which means the object will move 25 miles for every hour that passes.

An example of a ratio is 2 eggs:3 ounces of flour, which means the recipe calls for 2 eggs for every 3 ounces of flour used.

A statement that 2 rates or ratios are equal is a proportion.

For example, this is a proportion:

$\dfrac{2}{3}=\dfrac{8}{12}$

We can check if the proportion is correct by cross-multiplying

If we cross multiply, we get

$(2)(12)=(8)(3)$

which simplifies to

$24=24$

This proves that the proportion is correct.

Setting Up a Proportion

When setting up a proportion, always write down how you will set it up.

For example, if we know that someone reads 13 pages every 4 minutes, we can find out how many pages he would read in 22 minutes.

Write down how it would be set up first.
$\dfrac{pages}{minute}$

Then insert the values.

$\dfrac{13}{4}=\dfrac{x}{22}$

Use cross-multiplication to solve

$\dfrac{13}{4}=\dfrac{x}{22}$

becomes

$(13)(22)=(x)(4)$

Simplify to get

$286-4x$

Divide both sides by 4 to get

$71.5=x$

That means based on the rate, the person would read 71.5 pages in 22 minutes.

Problems with Ratios and a Total

A common type of proportion question on the SAT is a word problem in which a ratio is given. However, instead of giving you a value of one of the elements in the ratio, the question gives you the total of the elements in the ratio.

To solve for values when a ratio and a total is given, multiple each number in the ratio by x and then create an equation in which they all add up to the total. Then solve for x, and use that value of x to determine the other values.

Example

The ratio of boys to girls in a class is 2:3. If there are 45 students, how many boys are there?

Explanation & Solution

We know that the ratio of boys to girls is $2:3$ . That means the numbers could be 2 & 3, 4 & 6, 6 & 9. 8 & 12, etc.

What’s important is that whatever we multiply 2 by (for boys) we have to multiply 3 by (for girls). We can represent the number of boys as $2x$ and the number of girls as $3x$ .

We know that

(# of boys) + (# of girls) = (total # of students)

We can write the equation as

$2x+3x=45$

Combine like terms to get

$5x=45$

divide both sides by 5

$x=9$

This is not the answer. The question asks for the number of boys.

Number of boys is $2x$ , so $2(9) =18$ .

Use Matching Units in the Proportion

A way the SAT tests your knowledge of proportions is to mix up units on proportion questions.

Make sure to correct the units if they are different, before setting up the proportion.

Example

Tammy can read pages in minutes. How many pages can she read in hours?

Explanation & Solution

Let’s set up the proportion as $\dfrac{pages}{minute}$

Now, let’s set it up.

If we write

$\dfrac{10}{4}=\dfrac{x}{2}$

This would be incorrect because in the denominator on the left the 4 is in minutes and in the denominator on the right the 2 is in hours. The units don’t match up.

Let’s rewrite the 2 hours as 120 minutes, so both sides are using minutes.

$\dfrac{10}{4}=\dfrac{x}{120}$

Now, we can cross-multiply

$(10)(120)=(x)(4)$

Simplify

$1,200-4x$

Divide both sides by 4

$300=x$

Ratios Involving Formulas

On the SAT, you may be asked to compare the results of a formula when certain values are changed to an original value in the form of a ratio.

When given a formula, we can determine how one value will be affected by altering other values.

For example,

The weight of an object, $F_g$ , is found by multiplying the mass of an object, $m$ , by gravity, $g$ .
$F_g=mg$

If the mass, $m$ , is doubled, the weight, $F_g$ , will be doubled.

Just like when we solve equations, whatever we do to one side of the equation, we have to do to the other side of the equation.

Proportions in Shapes

Similar figures and shapes have proportionate side lengths.

A useful way to write down how we are setting up a proportion regarding geometric shapes is:

$\dfrac{Large}{Small}$

When dealing with proportionate shapes, make sure that you’re dealing with corresponding lengths. It is common for a question to ask for the length of a segment and not a full side.

Example

What is the value of $x$ in the figure below?

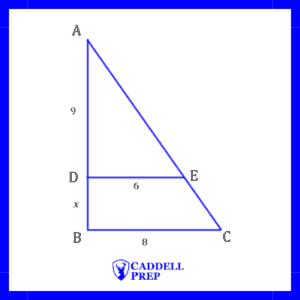
Explantation & Solution

Let’s set up the proportion as

$\dfrac{Large}{Small}$ ,

$x$ is not a length of the small or large triangle. 9 is the height of the small triangle. Let’s use $y$ to represent the height of the large triangle. After we solve for $y$ , we’ll be able to find the value of $x$ .

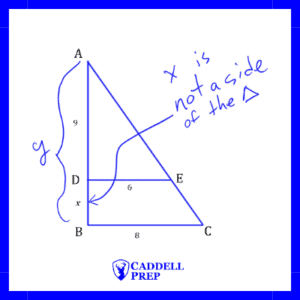
Now, we cans set up the proportion as

$\dfrac{Large}{Small}$ ,

$\dfrac{y}{9}=\dfrac{8}{6}$ ,

cross-multiply to get

$6y=72$ ,

divide both sides by 6

$y=12$

Remember than the question is asking for $x$ . $y$ is the total length.

To find $x$ we have to subtract 9 from $y$ .

$12-9=3$ ,

$x=3$

Data & Probability

On the SAT, Data & Probability is a big part of section 4 (Math: No Calculator). Mastering Data & Probability it an important step in improving your SAT score.

Bias in Surveys

It is common to see a question on the SAT that asks why a survey conducted is unreliable. Most of the times it is unreliable because of a possible bias related to who was surveyed, where they were surveyed, when they were surveyed, or how they were surveyed.

When choosing the group of people to be surveyed, the group should be a random sample of the entire population to be surveyed. For example, a survey to determine a town’s favorite pizzeria should randomly survey people from the town.

Most of the times, the answer won’t be because of the sample size.

Here are some examples of creating a bias based on who was surveyed:

A survey of the favorite class of students at a high school would not be reliable if only students from the freshmen class were surveyed or if any of the grades were excluded from the survey.
A survey of car enthusiasts to find out which car is the most popular would not be reliable if the survey was sent to a mailing list of people who earned a certain type of sports car.

Here are some examples of creating a bias based on location:

A survey of adults to determine the average number of children per household would not be reliable if the survey was done at a location where there are likely children because most of the adults there will have children. For example, at a playground the adults there are likely there with children, so it is less likely to survey an adult with no children.
A survey of people’s favorite activity would not be reliable if it was held at a place related to one of those activities. For example, at a movie theater the people are likely to choose going to the movies or at a bookstore the people are more likely to choose something related to reading.
A survey of whether people prefer watching sports in person or at home would not have reliable results if the survey was done outside a stadium before a game. The people there may be going to the game to watch it in person. Plus, it excludes the people who are home and waiting for the game to start.

Here are some examples of creating a bias based on when they were surveyed:

A survey of the most popular occupation in a town would not be reliable if people were randomly survey inside a supermarket on a weekday during the workday because people with professions that require them to work during normal work hours would be excluded from the survey.
A survey done to determine the opinion of the population of a town will likely not be reliable if done at a time when the majority of the population is expected to be sleeping.

An example of how a bias could be created is:

A survey that requires people to use a specific type of phone or through a specific social media application because it will exclude people who don’t have the specific type of phone of the specific application.

However, if the purpose is to survey owners of a specific phone, then it should be required that they use that type of phone to participate.

Scatterplots

Scatterplots are plots of data points (x,y). Common scatterplots are graphed against time, such as price vs. time, population vs. time, height vs. time, etc. In these cases, time is measured along the x-axis, and the other data along the y-axis. However, any comparison of data can be plotted; it doesn’t have to be against time.

On the SAT, questions involving scatterplots tend to include topics such as correlation, trendlines, and predicting data.

Correlation

When a relationship appears to exist among data points appear it is said that there is correlation.

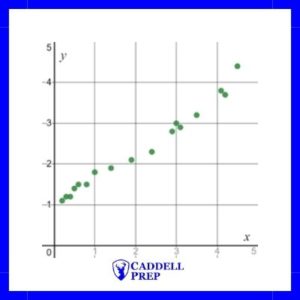
For example, as time increases, the cost of college increases. Since they both go up, it is said that there is positive correlation.

Below is an example of a positive correlation between x and y.

Another example would be as time increases the population of a specific species decreases. Since one value increases while the other decreases, it is said that there is a negative correlation.

Below is an example of a negative correlation between x and y.

The more apparent that there is a relationship, the stronger the correlation is said to be. Below are two examples of a negative correlation between and . However, the graph on the right shows a stronger correlation than the graph on the left.

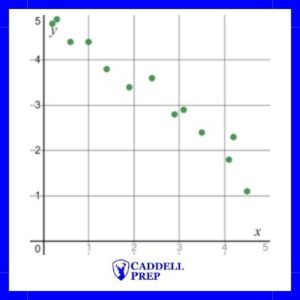
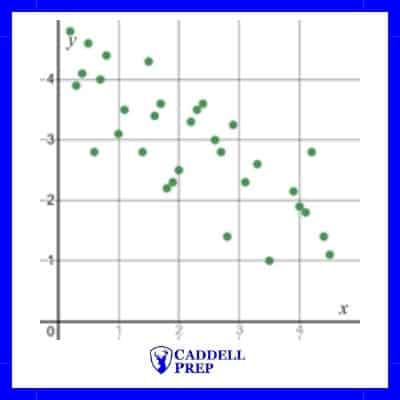Negative correlation

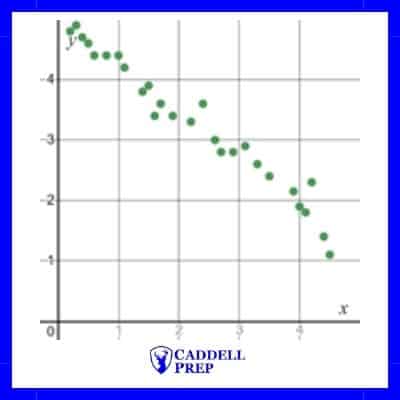Strong negative correlation

Trendlines

Trendlines (lines of best fit) can be applied to scatterplots that show correlation.

For example, a trendline has been added to the scatterplot below.

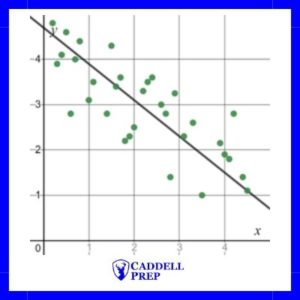
The line of best fit is modeled by $f(x)=-\dfrac{4}{5}x+4.7$ .

Obviously, each point on the scatterplot is not on the line of best fit. However, it does show the trend of the data and can be used to make estimations.

Based on the line of best fit, we can estimate the -value when is 4 by substituting into the function $f(x)=-\dfrac{4}{5}x+4.7$ .

$y=-\dfrac{4}{5}x+4.7$ ,

$y=-\dfrac{4}{5}(4)+4.7$ ,

$y=1.6$

If we look at the graph, we can see that when x is 4, y is approximately 1.9, not 1.6. It’s important to remember that we use the line of best, or a trendline, to estimate values.

Mean, Median, Mode, & Range

Mean (Average)

$Mean= \dfrac{Sum of Items}{Number of Items}$

For example, let’s find the mean of: 80, 90, 90, 95, 95

$Mean= \dfrac{80+90+90+95+95}{5}=90$

Many times, on the SAT it is important to be able to find the sum of the items in order to solve the problem.

Sum of Items=(Average)*(Number of Items)

Example

Mike’s average for 5 math tests is 90. His teacher is going to drop his lowest test, a 70. What will his average be for the remaining four tests?

Explanation & Solution

It is important to realize that we do not need to know what the other four test grades are. We only need to know what they add up to.

First let’s find his total including all 5 tests

Sum of Items=(Average)*(Number of Items)

$Sum=(90)\times(5)$ $Sum=450$

Now to find his new total, after dropping the 70, we simply have to subtract 70.

$New Sum=450-70$ $New Sum=380$

To find his new average we use the Arithmetic Mean (average) formula

Mean= (Sum of Items)/(Number of Items)

$Mean= \dfrac{380}{4}$ $Mean= 95$

Median, Mode, & Range

Median: The middle number in a set of numbers when arranged in order numerically.

Mode: The number that appears most often. It is possibly to have more than one mode.

Range: The difference between the largest number and the smallest number.

Example

Mary had the following bowling scores: 125, 215, 136, 195, and 202. How much greater is the median score than the mean?

Explanation & Solution

To find the median, put the scores in order and find the middle term.

In order, the scores are:

125, 136, 195, 202, 215

The median is 195.

Now let’s find the mean.

$Mean = \dfrac{125+136+195+202+215}{5}$

$Mean =\dfrac{873}{5}$ $Mean=174.6$

Now, we have to find the difference.

$195-174.6$ =20.4

Mean, Median, Mode, & Range from a Table

Sometimes on the SAT, data will be presented in a table. This makes the question slightly more difficult, partially because a table can include much more data than a list. Another reason it is complicated is students overlook the frequency of each value. Here are the methods for solving mean, median, mode and range questions on the SAT when the data is provided in a table.

Mean (Average) from a Table

Let’s look at the table of data provided.

Tests Scores	# of students
100	1
90	3
80	5
70	0
60	1
50	0

To find the mean from a table, total all of the rows and then divide by the total frequency of values.

We can find the total of the values by multiplying each value by the frequency then adding.

In the table above, there is one 100, three 90s, five 80s, etc. Instead of adding them individually, we can find the total of each row.

$100\times 1 =100$ ,

$90 \times 3 =270$ ,

$80 \times 5=400$ ,

$70 \times 0=0$ ,

$60\times 1=60$ ,

$50 \times 0=0$ ,

If we add all oof those up, we get 830.

If we add up the frequency column (# of students) we get 10.

Finally, we can find the mean (average).

$Mean=\dfrac{830}{10}$ ,

$Mean=830$

Median from a Table

To find the median, we don’t want to write out all of the values.

Instead, we want to determine which term will be the middle term from the table.

To find which term will be the median, use the following formula

$Median Term=\dfrac{n+1}{2}$

Where $n$ is the number of terms. Note: If there is an even number of terms, we will get an answer that ends in “.5”. This means the median is the average of the numbers in the places before and after.

Example
If there are 13 numbers, which one will be the median?

Explanation & Solution

Let’s use the formula

$Median Term=\dfrac{n+1}{2}$ ,

$Median Term=\dfrac{13+1}{2}$ ,

$Median Term=\dfrac{14}{2}$ ,

$Median Term=7$ ,

The median is the 7th term.

Mode from a Table

Let’s look at an example of finding the mode from a table of data.

Tests Scores	# of students
100	1
90	3
80	5
70	0
60	1
50	0

Mode is the easiest to find from a table, but still trips up some students.

The value with the greatest frequency is the mode, so in this case 80 is the mode because 5 students scored an 80 (the frequency is 5).

Some student might get tripped up and pick 0 or 1 because they appear the most, twice.

However, we have to realize that the second column represents frequencies.

Really, this is the data in the table:

100, 90, 90, 90, 80, 80, 80, 80, 80, 60

Now, it is clearer that the mode is 80.

Range from a Table

Below is a table of data that shows the frequency of test scores for a class.

Test Scores	# of students
100	1
90	3
80	5
70	0
60	1
50	0

Finding the range from a table is fairly straight forward, simply find the difference between the highest value and the lowest.

Be certain to subtract values and not frequencies.

Also, make sure the value exists in the data set. For example, if we look at the table above, it looks like 50 is the lowest value, so the range would be 100-50=50.

However, there are no 50s (the frequency is 0), so the lowest test score is actually 60.

The range is 100-60=40.

Drawing Appropriate Conclusions

One of the most important things to remember about drawing conclusions from a survey is that we can only infer what it likely true about the entire population of that group.

For example, if a survey of 50 8^th graders from a school in New York City reveals that 40% of the students surveyed like football more than baseball, we can infer that it is likely that 40% of the entire 8^th grade class in that school likes football more than baseball. However, it would be in correct to apply that information to the entire school since only 8^th graders were surveyed, and it would be wrong to apply that information to all 8^th graders in New York City because only 8^th graders from one school were surveyed.

Filling in Tables

Sometimes data will be presented in a table. In those tables one column and/or one row may represent totals.

The values should add up correctly and give the right totals.

For example, let’s look at the following table

	Saw the Movie	Didn’t See the Movie	Total
Men	58	192	250
Women	238	12	250
Total	296	204	500

The columns add up.

The column “Saw the Movie” adds up, 58+238=296

The column “Didn’t see the Movie” adds up, 192+12=204

The last column “Total” adds us, 250+250=500

The rows also add up.

The row for “Men” adds up, 58+192=250.

The row for “Women” adds up, 238+12=250.

The row for “Total” adds up, 296+204=500.

Since we can add up the values, we can solve for missing values.

Probability

Probability is the likeliness of something occurring.

For example, if you roll a die, there is a 1/6 chance of it landing on 3.

Probabilty=(# of favorable outcomes)/(total possible outcomes)

For rolling a 3, there is only one 3 on a die, so the number of favorable outcomes is 1. There are 6 possible outcomes, so the number of total possible outcomes is 6. Therefore, the probability is 1/6.

Probability can be expressed as a fraction, a decimal or a percent.

1/6=0.167=16.7%

Example

Television Programs Watched Each Week

	None	1 to 3	4 or more	Total
Group A	5	38	57	100
Group B	7	45	48	100
Total	12	83	105	200

For a science project, a student interviewed 200 people. Group A consisted of 100 adults and Group B consisted of 100 high school students.

Part 1

If a person is chosen at random from Group A, what is the probability that the person watches 4 or more television programs each week?

Part 2

If a person is chosen at random from those who watch at least 1 television program per week, what is the probability that the person belonged to Group B?

Part 3

If a person who participated in the science project is chosen at random, what is the probability that the person was from Group A and watched 1 to 3 television programs per week?

Explanation & Solution

Part 1

A person is chosen at random from Group A, so a person will be chose out of 100 people. This will be the denominator.

In Group A, there are 57 people who watch 4 hours or more, so there are 57 favorable outcomes.

The probability of selecting a person that watches 4 or more hours of television from Group A is 57/100 or 0.57.

Part 2

A person is chosen at random from those who watch at least 1 hour of television per week. At least one hour per week includes the people who watch 1-3 hours per week and 4 or more hours per week.

We have to add the 83 people who watch 1-3 hours per week and the 105 people who watch 4 or more hours per week to get a total of 188 people that we are selecting from. 188 will be the denominator.

We need to find the probability of selecting someone from Group B out of the 188 people, so we need to find the number of people in Group B who watch at least 1 hour of television per week. In Group B, 45 people watch 1-3 hours of television per week and 48 watch 4 or more hours of television per week, so there are 93 people in Group B who watch at least 1 hour of television per week.

The probability of selecting a person from Group B from the people who watch at least 1 hour of television per week is 93/188 or as a decimal it could be written as .494 or .495.

Part 3

For Part 3 of this SAT example, a person is chosen randomly from the project, so a person is chosen at random from all 200 participants. The denominator will be 200.

The question is asking for the probability of selecting someone from Group A who watches 1-3 hours per week. There are 38 people in Group A who watch television 1-3 hours per week, so the probability is 38/200, which reduces to 19/100 or .19.

Standard Deviation

In many cases, values tend to be centrally located.

For example, the test grades of a class might be as follows:

Test Grade	Frequency
70	2
75	3
80	5
85	12
90	7
95	2
100	1

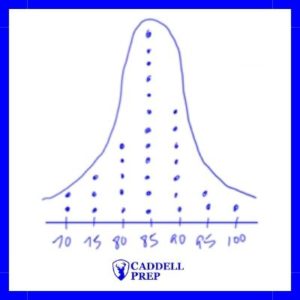
The average test grade in the class is 84.5. From the table, we can see that most of the test grades are close to 84.5.

A dot plot of the data would give us the following:

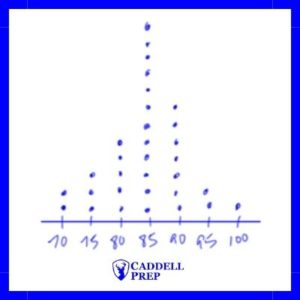
If follows a bell shape.

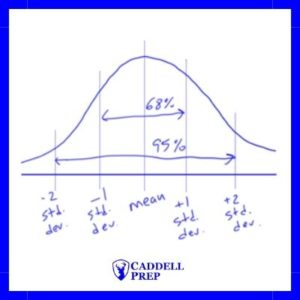
When data is normally distributed, we can use standard deviation to make estimates about the data. Two concepts that come up on the SAT are: about 68% of the values are estimated to be within one standard deviation of the mean and about 95% of the values are estimated to be within two standard deviation of the mean.

For example, if the mean chemistry final exam score for a school is 78 and the standard deviation is 6, we can estimate that 65% of the students scored between 72 (6 less than the mean) and 84 (6 greater than the mean. 95% of the values will be within two standard deviations (12) of the mean, so we can estimate that 95% of the students scored between 66 (12 less than the mean) and 90 (12 more than the mean).

Below is a diagram to help show the concept visually.

For example, below are the grades for two classes. Both classes have 23 students, a low score of 75, and a high score of 100. However, they have different standard deviations.

Class A		Class B
Test Score	Frequency	Test Score	Frequency
75	1	75	5
80	3	80	4
85	5	85	2
90	8	90	5
95	4	95	3
100	2	100	4

Most of the scores in Class A are between 85 and 95. But the scores in Class B are spread throughout the range. As a result, the standard deviation of Class A’s scores is smaller than the standard deviation of Class B’s scores.

Average Increase/Decrease

To find the average increase or decrease of a value over time, we just have to focus on the initial and final values.

Let’s look at this graph that shows the price of an item over time.

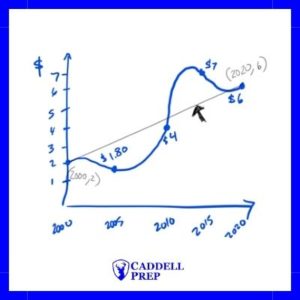
The price changed at different rates at different times. In fact, at times the price was increasing and at other times it was decreasing.

We can find the average increase or decrease by finding the slope of the line drawn from start to finish.

Rate of change = slope

$slope=\dfrac{y_2-y_1}{x_2-x_1}$ ,

$slope=\dfrac{6-2}{2020-2000}$ ,

$slope=0.2$

The average increase is $0.20/year.

We can find the average change from a table also.

Example

Year	Average Home Price ($)
1970	180,000
1980	195,000
1990	220,000
2000	250,000
2010	205,000
2020	230,000

The table above shows the average home prices in Makebelieveville. What is the average annual increase in average home prices from 1980 to 2010?

Explanation a& Solution

In 1980, the average was $195,000.

In 2010, the average was $204,000.

Since we are looking for the average annual increase, we need to find the change in price per year.

Rate of change = slope

$slope=\dfrac{y_2-y_1}{x_2-x_1}$ ,

$slope=\dfrac{205,000-195,000}{2010-1980}$ ,

$slope=\dfrac{10,000}{30}$ ,

$slope =333.33$

Annual increase of $333.33

Table of Contents

Rates, Ratios & Proportions

What are Rates, Ratios, and Proportions?

Setting Up a Proportion

Problems with Ratios and a Total

Use Matching Units in the Proportion

Ratios Involving Formulas

Proportions in Shapes

Data & Probability

Bias in Surveys

Scatterplots

Correlation

Trendlines

Mean, Median, Mode, & Range

Mean (Average)

Median, Mode, & Range

Mean, Median, Mode, & Range from a Table

Mean (Average) from a Table

Median from a Table

Mode from a Table

Range from a Table

Drawing Appropriate Conclusions

Filling in Tables

Probability

Standard Deviation

Average Increase/Decrease