June 2018 Geometry Regents

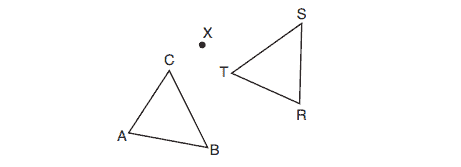
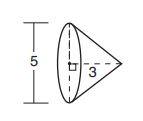1. After a counterclockwise rotation about point $X$ , scalene triangle $ABC$ maps onto $\triangle RST$ , as shown in the diagram below.

Which statement must be true?

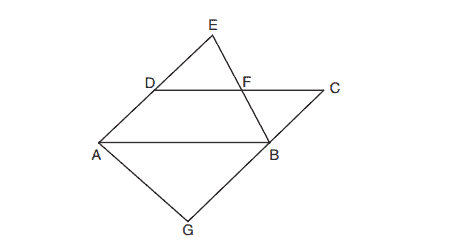
(1) $\angle A \cong \angle R$
(2) $\angle A \cong \angle S$
(3) $\overline{CB} \cong \overline{TR}$
(4) $\overline{CA} \cong \overline{TS}$

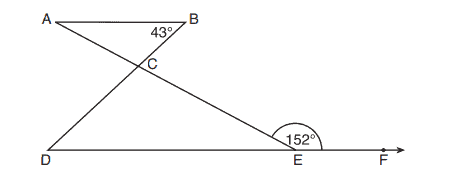
2. In the diagram below, $\overline{AB} \| \overline{DEF}$ , $\overline{AE}$ , and $\overline{BD}$ at $C$ , $m\angle B = 43^{\circ}$ , and $m\angle CEF = 152^{\circ}$ .

Which statement is true?

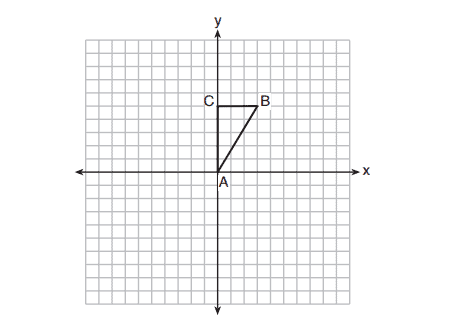
(1) $m\angle D = 28^{\circ}$
(2) $m\angle A = 43^{\circ}$
(3) $m\angle ACD = 71^{\circ}$
(4) $m\angle BCE = 109^{\circ}$

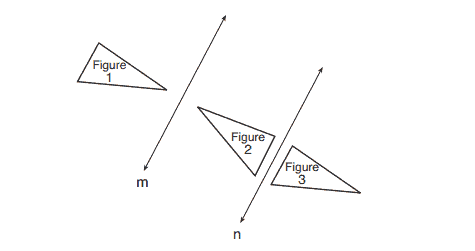
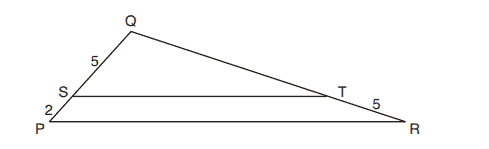
3. In the diagram below, line $m$ is parallel to line $n$ . Figure 2 is the image of Figure 1 after a reflection over line $m$ . Figure 3 is the image of Figure 2 after a reflection over line $n$ .

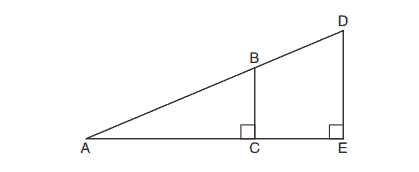
Which single transformation would carry Figure 1 onto Figure 3?

(1) a dilation
(2) a rotation
(3) a reflection
(4) a translation

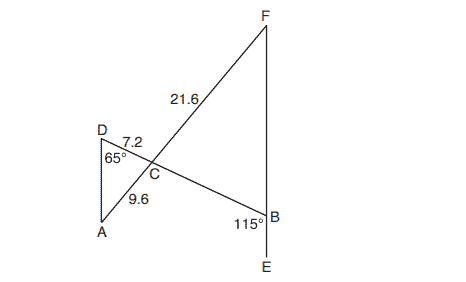
4. In the diagram below, $\overline{AF}$ and $\overline{DB}$ intersect at $C$ , and $\overline{AD}$ and $\overline{FBE}$ are drawn such that $m\angle D = 65^{\circ}$ , $m\angle CBE = 115^{\circ}$ , $DC = 7.2$ , $AC = 9.6$ , and $FC = 21.6$ .

What is the length of $\overline{CB}$ ?

(1) $3.2$
(2) $4.8$
(3) $16.2$
(4) $19.2$

5. Given square $RSTV$ , where $RS = 9$ cm. If square $RSTV$ is dilated by a scale factor of $3$ about a given center, what is the perimeter, in centimeters, of the image of $RSTV$ after the dilation?

(1) $12$
(2) $27$
(3) $36$
(4) $108$

6. In right triangle $ABC$ , hypotenuse $\overline{AB}$ has a length of $26$ cm, and side $\overline{BC}$ has a length of $17.6$ cm. What is the measure of angle $B$ , to the nearest degree?

(1) $48^{\circ}$
(2) $47^{\circ}$
(3) $43^{\circ}$
(4) $34^{\circ}$

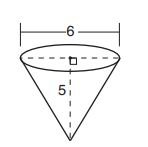
7. The greenhouse pictured below can be modeled as a rectangular prism with a half-cylinder on top. The rectangular prism is $20$ feet wide, $12$ feet high, and $45$ feet long. The half-cylinder has a diameter of $20$ feet.

To the nearest cubic foot, what is the volume of the greenhouse?

(1) $17,869$
(2) $24,937$
(3) $39,074$
(4) $67,349$

8. In a right triangle, the acute angles have the relationship $sin (2x + 4) = cos (46)$ . What is the value of $x$ ?

(1) $20$
(2) $21$
(3) $24$
(4) $25$

9. In the diagram below, $\overline{AB} \| \overline{DFC}$ , $\overline{EDA} \| \overline{CBG}$ , and $\overline{EFB}$ and $\overline{AG}$ are drawn.

Which statement is always true?

(1) $\triangle DEF \cong \triangle CBF$
(2) $\triangle BAG \cong \triangle BAE$
(3) $\triangle BAG \sim \triangle AEB$
(4) $\triangle DEF \sim \triangle AEB$

10. The base of a pyramid is a rectangle with a width of $4.6$ cm and a length of $9$ cm. What is the height, in centimeters, of the pyramid if its volume is $82.8$ cm $^{3}$ ?

(1) $6$
(2) $2$
(3) $9$
(4) $18$

11. In the diagram below of right triangle $AED$ , $\overline{BC} \| \overline{DE}$ .

Which statement is always true?

(1) $\dfrac{AC}{BC} = \dfrac{DE}{AE}$
(2) $\dfrac{AC}{BC} = \dfrac{DE}{AE}$
(3) $\dfrac{AC}{CE} = \dfrac{BC}{DE}$
(4) $\dfrac{DE}{BC} = \dfrac{DB}{AB}$

12. What is an equation of the line that passes through the point ( $6,8$ ) and is perpendicular to a line with equation $y = \dfrac{3}{2}x + 5$ ?

(1) $y - 8 = \dfrac{3}{2}(x - 6)$
(2) $y - 8 = -\dfrac{2}{3}(x - 6)$
(3) $y + 8 = \dfrac{3}{2}(x + 6)$
(4) $y + 8 = -\dfrac{2}{3}(x + 6)$

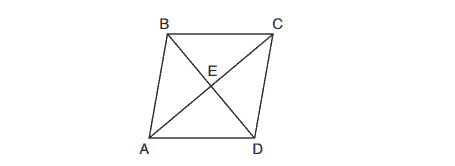
13. The diagram below shows parallelogram $ABCD$ with diagonals $\overline{AC}$ and $\overline{BD}$ intersecting at $E$ .

What additional information is sufficient to prove that parallelogram $ABCD$ is also a rhombus?

(1) $\overline{BD}$ bisects $\overline{AC}$
(2) $\overline{AB}$ is parallel to $\overline{CD}$
(3) $\overline{AC}$ is congruent to $\overline{BD}$
(4) $\overline{AC}$ is perpendicular to $\overline{BD}$

14. Directed line segment $DE$ has endpoints $D(-4,-2)$ and $E(1,8)$ . Point $F$ divides $\overline{DE}$ such that $DF : DE$ is $2:3$ . What are the coordinates of $F$ ?

(1) ( $-3, 0$ )
(2) ( $-2, 2$ )
(3) ( $-1, 4$ )
(4) ( $2, 4$ )

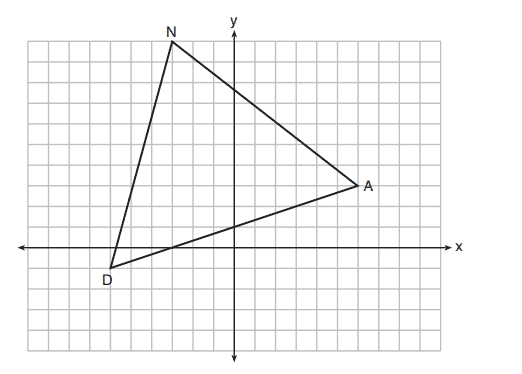
15. Triangle $DAN$ is graphed on the set of axes below. The vertices of $\triangle DAN$ have coordinates $D (-6, -1)$ , $A (6, 3)$ , and $N (-3, 10)$ .

What is the area of $\triangle DAN$ ?

(1) $60$
(2) $120$
(3) $20\sqrt{13}$
(4) $40\sqrt{13}$

16. Triangle $ABC$ , with vertices at $A(0,0)$ , $B(3,5)$ , and $C(0,5)$ , is graphed on the set of axes shown below.

Which figure is formed when $\triangle ABC$ is rotated continuously about $\overline{BC}$ ?

(1)
(2)
(3)
(4)

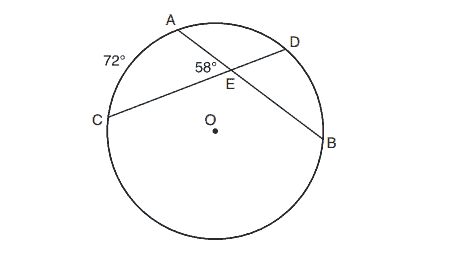
17. In the diagram below of circle $O$ , chords $\overline{AB}$ and $\overline{CD}$ intersect at $E$ .

If $m\widehat{AC} = 72^{\circ}$ and $m\angle AEC = 58^{\circ}$ , how many degrees are in $m\widehat{DB}$ ?

(1) $108^{\circ}$
(2) $65^{\circ}$
(3) $44^{\circ}$
(4) $14^{\circ}$

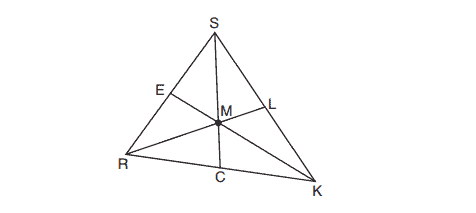
18. In triangle $SRK$ below, medians $\overline{SC}$ , $\overline{KE}$ , and $\overline{RL}$ intersect at $M$ .

Which statement must always be true?

(1) $3(MC) = SC$
(2) $MC = \dfrac{1}{3}(SM)$
(3) $RM = 2MC$
(4) $SM = KM$

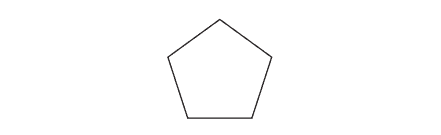
19. The regular polygon below is rotated about its center.

Which angle of rotation will carry the figure onto itself?

(1) $60^{\circ}$
(2) $108^{\circ}$
(3) $216^{\circ}$
(4) $540^{\circ}$

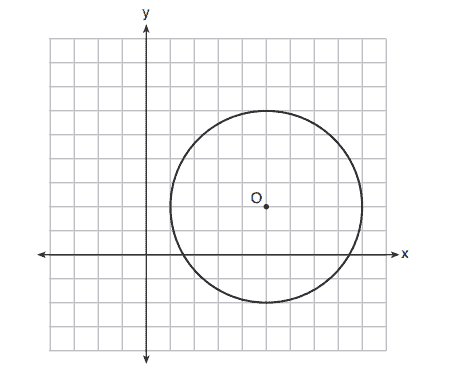
20. What is an equation of circle $O$ shown in the graph below?

(1) $x^{2} + 10x + y^{2} + 4y = -13$
(2) $x^{2} - 10x + y^{2} - 4y = -13$
(3) $x^{2} + 10x + y^{2} + 4y = -25$
(4) $x^{2} - 10x + y^{2} + 4y = -25$

21. In the diagram below of $\triangle PQR$ , $\overline{ST}$ is drawn parallel to $\overline{PR}$ , $PS = 2$ , $SQ = 5$ , and $TR = 5$ .

What is the length of $\overline{QR}$ ?

(1) $7$
(2) $2$
(3) $12\dfrac{1}{2}$
(4) $17\dfrac{1}{2}$

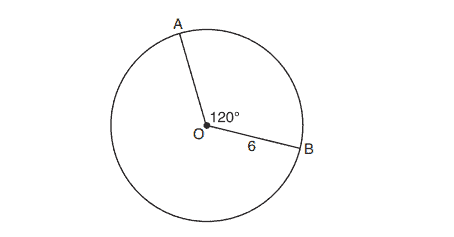
22. The diagram below shows circle $O$ with radii $\overline{OA}$ and $\overline{OB}$ . The measure of angle $AOB$ is $120^{\circ}$ , and the length of a radius is $6$ inches.

Which expression represents the length of arc $AB$ , in inches?

(1) $\dfrac{120}{360} (6\pi)$
(2) $120 (6)$
(3) $\dfrac{1}{3} (36\pi)$
(4) $\dfrac{1}{3} (12\pi)$

23. Line segment $CD$ is the altitude drawn to hypotenuse $\overline{EF}$ in right triangle $ECF$ . If $EC = 10$ and $EF = 24$ , then, to the nearest tenth, $ED$ is

(1) $4.2$
(2) $5.4$
(3) $15.5$
(4) $21.8$

24. Line $MN$ is dilated by a scale factor of $2$ centered at the point ( $0, 6$ ). If $\overline{MN}$ is represented by $y = -3x + 6$ , which equation can represent $\overline{M'N'}$ , the image of $\overline{MN}$ ?

(1) $y = -3x + 12$
(2) $y = -3x + 6$
(3) $y = -6x + 12$
(4) $y = -6x + 6$