June 2018 Algebra One Regents

Answer all 24 questions in this part. Each correct answer will receive 2 credits. No partial credit will be allowed. Utilize the information provided for each question to determine your answer. Note that diagrams are not necessarily drawn to scale. For each statement or question,
choose the word or expression that, of those given, best completes the statement or answers the question. Record your answers on your separate answer sheet.

Part I – Multiple Choice

1. The solution to $4p + 2 \textless 2(p + 5)$ is

(1) $p \textgreater -6$
(2) $p \textless -6$
(3) $p \textgreater 4$
(4) $p \textless 4$

2. If $k(x) = 2x^{2} - 3 \sqrt{x}$ , then $k(9)$ is

(1) $315$
(2) $307$
(3) $159$
(4) $153$

3. The expression $3 (x^{2} + 2x - 3) - 4 (4x^{2} - 7x + 5)$ is equivalent to

(1) $-13x - 22x + 11$
(2) $-13x^{2} + 34x - 29$
(3) $19x^{2} - 22x + 11$
(4) $19x^{2} +34x - 29$

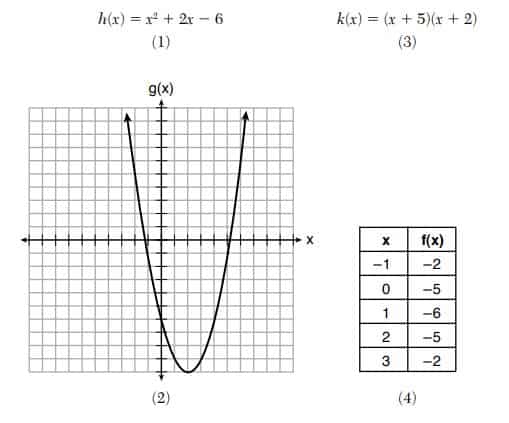
4. The zeros of the function $p(x) = x^{2} - 2x - 24$ are

(1) $-8$ and $3$
(2) $-6$ and $4$
(3) $-4$ and $6$
(4) $-3$ and $8$

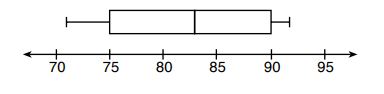
5. The box plot below summarizes the data for the average monthly high temperatures in degrees Fahrenheit for Orlando, Florida.

The third quartile is

(1) $92$
(2) $90$
(3) $83$
(4) $71$

6. Joy wants to buy strawberries and raspberries to bring to a party. Strawberries cost $\$1.60$ per pound and raspberries cost $\$1.75$ per pound. If she only has $\$10$ to spend on berries, which inequality represents the situation where she buys $x$ pounds of strawberries and $y$ pounds of raspberries?

(1) $1.60x + 1.75y \leq 10$
(2) $1.60x + 1.75y \geq 10$
(3) $1.75x + 1.60y \leq 10$
(4) $1.75x + 1.60y \geq 10$

7. On the main floor of the Kodak Hall at the Eastman Theater, the number of seats per row increases at a constant rate.
Steven counts $31$ seats in row $3$ and $37$ seats in row $6$ . How many seats are there in row $20$ ?

(1) $65$
(2) $67$
(3) $69$
(4) $71$

8. Which ordered pair below is not a solution to $f(x) = x^{2} - 3x + 4$ ?

(1) $(0, 4)$
(2) $(1.5, 1.75)$
(3) $(5, 14)$
(4) $(-1, 6)$

9. Students were asked to name their favorite sport from a list of basketball, soccer, or tennis. The results are shown in the table below.

What percentage of the students chose soccer as their favorite sport?

(1) $39.6\%$
(2) $41.4\%$
(3) $50.4\%$
(4) $58.6\%$

10. The trinomial $x^{2} - 14x + 49$ can be expressed as

(1) $(x - 7)^{2}$
(2) $(x + 7)^{2}$
(3) $(x - 7) (x + 7)$
(4) $(x - 7) (x + 2)$

11. A function is defined as ${(0,1), (2,3), (5,8), (7,2)}$ . Isaac is asked to create one more ordered pair for the function. Which ordered pair can he add to the set to keep it a function?

(1) $(0, 2)$
(2) $(5, 3)$
(3) $(7, 0)$
(4) $(1, 3)$

12. The quadratic equation $x^{2} - 6x = 12$ is rewritten in the form $(x + p)^{2} = q$ , where $q$ is a constant. What is the value of $p$ ?

(1) $-12$
(2) $-9$
(3) $-3$
(4) $9$

13. Which of the quadratic functions below has the smallest minimum value?

14. Which situation is not a linear function?

(1) A gym charges a membership fee of $\$10.00$ down and $\$10.00$ per month.
(2) A cab company charges $\$2.50$ initially and $\$3.00$ per mile.
(3) A restaurant employee earns $\$12.50$ per hour.
(4) A $\$12,000$ car depreciates $15\%$ per year.

15. The Utica Boilermaker is a $15$ -kilometer road race. Sara is signed up to run this race and has done the following training runs:

I. $10$ miles
II. $44,880$ feet
III. $15,560$ yards

Which run(s) are at least $15$ kilometers?

(1) I, only
(2) II, only
(3) I and III
(4) II and III

16. If $f(x) = x^{2} + 2$ , which interval describes the range of this function?

(1) $(-\infty, \infty)$
(2) $(0, \infty)$
(3) $(2, \infty)$
(4) $(-\infty, 2)$

17. The amount Mike gets paid weekly can be represented by the expression $2.50a + 290$ , where $a$ is the number of cell phone accessories he sells that week. What is the constant term in this expression and what does it represent?

(1) $2.50a$ , the amount he is guaranteed to be paid each week
(2) $2.50a$ , the amount he earns when he sells $a$ accessories
(3) $290$ , the amount he is guaranteed to be paid each week
(4) $290$ , the amount he earns when he sells $a$ accessories

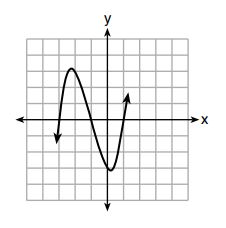
18. A cubic function is graphed on the set of axes below.

Which function could represent this graph?
(1) $f(x) = (x - 3) (x - 1) (x +1)$
(2) $g(x) = (x + 3) (x + 1) (x -1)$
(3) $h(x) = (x - 3) (x - 1) (x + 3)$
(4) $k(x) = (x + 3) (x + 1) (x - 3)$

19. Mrs. Allard asked her students to identify which of the polynomials below are in standard form and explain why.

I. $15x^{4} - 6x + 3x^{2} - 1$
II. $12x^{3} + 8x + 4$
III. $2x^{5} + 8x^{2} + 10x$

Which student’s response is correct?
(1) Tyler said I and II because the coefficients are decreasing.
(2) Susan said only II because all the numbers are decreasing.
(3) Fred said II and III because the exponents are decreasing.
(4) Alyssa said II and III because they each have three terms.

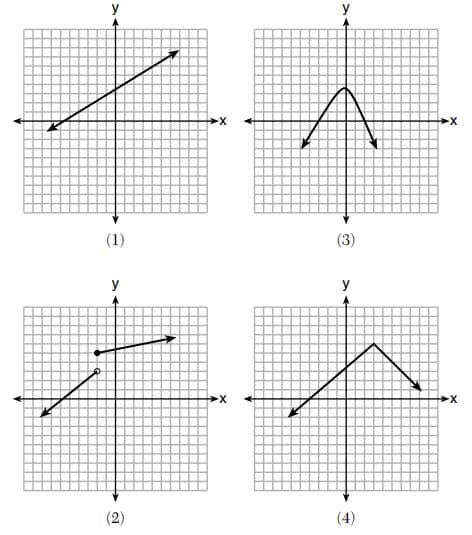
20. Which graph does not represent a function that is always increasing over the entire interval $-2 \textless x \textless 2$ ?

21. At an ice cream shop, the profit, $P(c)$ , is modeled by the function computations.
$P(c) = 0.87c$ , where $c$ represents the number of ice cream cones sold. An appropriate domain for this function is

(1) an integer $\leq 0$
(2) an integer $\geq 0$
(3) a rational number $\leq 0$
(4) a rational number $\geq 0$

22. How many real-number solutions does $4x^{2} + 2x + 5 = 0$ have?

(1) one
(2) two
(3) zero
(4) infinitely many

23. Students were asked to write a formula for the length of a rectangle by using the formula for its perimeter, $p = 2\ell + 2w$ . Three of their responses are shown below.