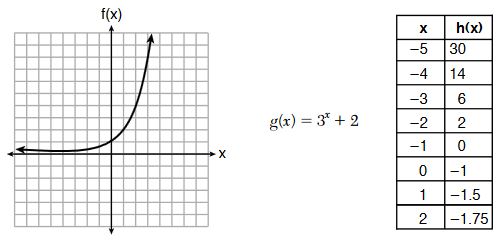Answer all 24 questions in this part. Each correct answer will receive 2 credits. No partial credit will be allowed. Utilize the information provided for each question to determine your answer. Note that diagrams are not necessarily drawn to scale. For each statement or question,
choose the word or expression that, of those given, best completes the statement or answers the question. Record your answers on your separate answer sheet.
You need to be registered and logged in to take this quiz. Log in
Part I – Multiple Choice
1. The number of bacteria growth in a lab can be modeled by , where
is the number of hours. Which expression is equivalent to
?
(1)
(2)
(3)
(4)
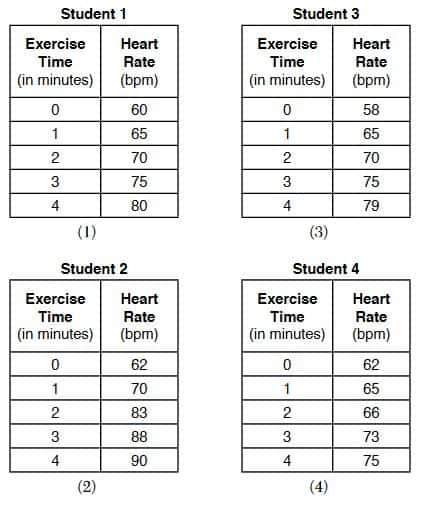
2. During physical education class, Andrew recorded the exercise times in minutes and heart rates in beats per minute (bpm) of four of his classmates. Which table best represents a linear model of exercise time and heart rate?
3. David correctly factored the expression . Which expression did he write?
(1)
(2)
(3)
(4)
4. The solution to is
(1)
(2)
(3)
(4)
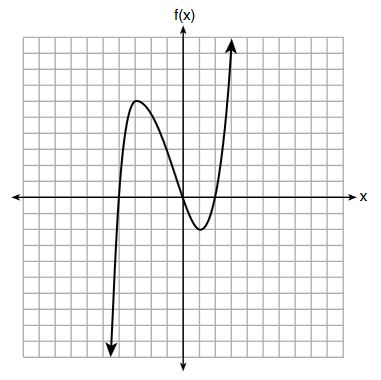
5. The graph of is shown below.
What is the value of ?
(1)
(2)
(3)
(4)
6. If the function has the domain {
}, what is its range?
(1)
(2)
(3)
(4)
7. The expression is equivalent to
(1)
(2)
(3)
(4)
8. Compared to the graph of , the graph of
is the result of translating
(1) units up and
units right
(2) units down and
units up
(3) units right and
units up
(4) units left and
units right
9. Lizzy has coins that total
. All of her coins are dimes,
, and quarters,
. Which system of equations models this situation?
(1) ,
(2) ,
(3) ,
(4) ,
10. Gretchen has that she can spend at the fair. Ride tickets cost
each and game tickets cost
each. She wants to go on a minimum of
rides and play at least
games.
Which system of inequalities represents this situation when r is the number of ride tickets purchased and g is the number of game tickets purchased?
(1) ,
,
(2) ,
,
(3) ,
,
(4) ,
,
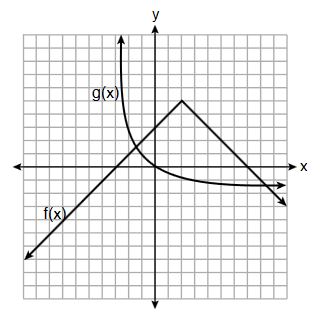
11. Three functions are shown below.
Which statement is true?
(1) The -intercept for
is greater than the
-intercept for
.
(2) The -intercept for
is greater than the
-intercept for
.
(3) The -intercept for
is greater than the
-intercept for both
and
.
(4) The -intercept for
is greater than the
-intercept for both
and
.
12. Olivia entered a baking contest. As part of the contest, she needs to demonstrate how to measure a gallon of milk if she only has a teaspoon measure. She converts the measurement using the ratios below:
Which ratio is incorrectly written in Olivia’s conversion?
(1)
(2)
(3)
(4)
13. If and
, which polynomial is equivalent to
?
(1)
(2)
(3)
(4)
14. An outdoor club conducted a survey of its members. The members were asked to state their preference between skiing and snowboarding. Each member had to pick one. Of the males,
stated they preferred to snowboard. Twenty-two of the
females preferred to ski. What is the relative frequency that a male prefers to ski?
(1)
(2)
(3)
(4)
15. When the function is graphed correctly, how should the points be drawn on the graph for an
-value of
?
(1) open circles at and
(2) closed circles at and
(3) an open circle at and a closed circle at
(4) a closed circle at and an open circle at
16. If , which equation can be used to determine the zeros of the function?
(1)
(2)
(3)
(4)
17. Each day, a local dog shelter spends an average of on food per dog. The manager estimates the shelter’s daily expenses, assuming there is at least one dog in the shelter, using the function
.
Which statements regarding the function are correct?
I. represents the number of dogs at the shelter per day.
II. represents the number of volunteers at the shelter per day.
III. represents the shelter’s total expenses per day.
IV. represents the shelter’s nonfood expenses per day.
(1) I and III
(2) I and IV
(3) II and III
(4) II and IV
18. Which point is not in the solution set of the equation ?
(1)
(2)
(3)
(4)
19. The functions and
are graphed below.
Based on the graph, the solutions to the equation are
(1) the -intercepts
(2) the -intercepts
(3) the -values of the points of intersection
(4) the -values of the points of intersection
20. For the sequence -27, -12, 3, 18, …, the expression that defines the th term where
is
(1)
(2)
(3)
(4)
21. The data obtained from a random sample of track athletes showed that as the foot size of the athlete decreased, the average running speed decreased. Which statement is best supported by the data?
(1) Smaller foot sizes cause track athletes to run slower.
(2) The sample of track athletes shows a causal relationship between foot size and running speed.
(3) The sample of track athletes shows a correlation between foot size and running speed.
(4) There is no correlation between foot size and running speed in track athletes.
22. Which system of equations will yield the same solution as the system below?
,
(1) ,
(2) ,
(3) ,
(4) ,
23. Which of the three situations given below is best modeled by an exponential function?
I. A bacteria culture doubles in size every day.
II. A plant grows by 1 inch every 4 days.
III. The population of a town declines by 5% every 3 years.
(1) I, only
(2) II, only
(3) I and II
(4) I and III
24. The length, width, and height of a rectangular box are represented by and
, respectively. When the volume is expressed as a polynomial in standard form, what is the coefficient of the 2nd term?
(1)
(2)
(3)
(4)