2018 Grade 7 Math Regents

1. What is the decimal equivalent of the fraction $\dfrac{8}{15}$ ?

A. $0.53$
B. $0.5\overline{3}$
C. $0.\overline{53}$
D. $0.533$

2. The circumference of a circle is $15\pi$ centimeters. What is the area of the circle in terms of $\pi$ ?

A. $7.5\pi cm^2$
B. $15\pi cm^2$
C. $56.25\pi cm^2$
D. $225\pi cm^2$

3. Bob buys eggs and potatoes at a store.

$\bullet$ He pays a total of $\$25.92$ .
$\bullet$ He pays $\$2.57$ for the eggs.
$\bullet$ He buys $5$ bags of potatoes that each cost the same amount.

Which equation can be used to determine the cost, $x$ , of each bag of potatoes?

A. $x=(25.92 - 2.57)\div 5$
B. $x=25.92 \div 5 + 2.57$
C. $x=(25.92 + 2.57)\div 5$
D. $x=25.92 \div 5 - 2.57$

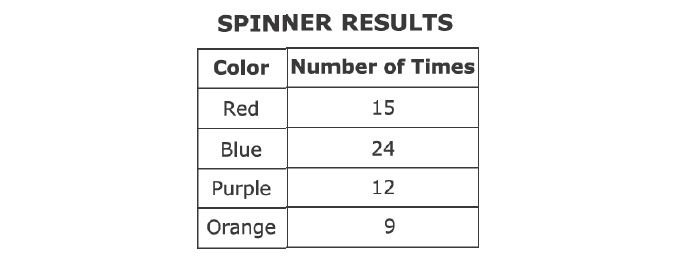
6. A spinner is divided into four colored sections that are not of equal size: red, blue, purple, and orange. The arrow on the spinner is spun several times.

The arrow on the spinner will be spun one more time. Based on these results, what is the probability that the arrow will land on the purple section?

A. $\dfrac{1}{4}$
B. $\dfrac{1}{5}$
C. $\dfrac{1}{6}$
D. $\dfrac{1}{12}$

7. The table below shows the lowest temperature, in degrees Fahrenheit, on each of $5$ days for a city.

What is the mean lowest temperature, in degrees Fahrenheit, in the city for those $5$ days?

A. $-18.8^{\circ}$
B. $-6.8^{\circ}$
C. $6.8^{\circ}$
D. $18.8^{\circ}$

10. Which expression is equivalent to $(-18) - 64n$ ?

A. $-2(9 - 32n)$
B. $2(9 - 32n)$
C. $-2(9 + 32n)$
D. $2(9 + 32n)$

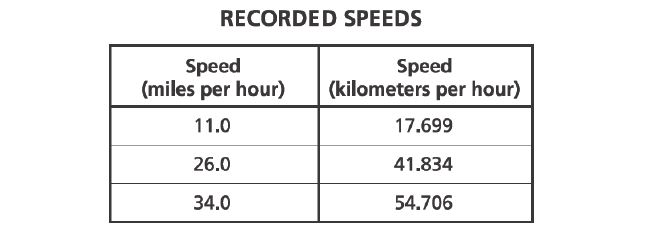
11. Verda used a sensor to measure the speed of a moving car at different times. At each time, the sensor measured the speed of the car in both miles per hour and kilometers per hour. The table below shows her results.

Based on her results, which statement describes the relationship between $m$ , the speed of the car in miles per hour, and $k$ , the speed of the car in kilometers per hour?

A. The relationship is proportional because the ratio of $m$ to $k$ is constant.
B. The relationship is not proportional because the ratio of $m$ to $k$ is constant.
C. The relationship is proportional because the difference between $m$ and $k$ is constant.
D. The relationship is not proportional because the difference between $m$ and $k$ is constant.

16. Bonnie deposits $\$70.00$ into a new savings account.

$\bullet$ The account earns $4.5\%$ simple interest per year.
$\bullet$ No money is added or removed from the savings account for $3$ years.

What is the total amount of money in her savings account at the end of the $3$ years?

A. $\$9.45$
B. $\$79.45$
C. $\$94.50$
D. $\$164.50$

17. Which situation results in a final value of zero?

A. The temperature after a decrease of $5^{\circ}$ F from a temperature of $-5^{\circ}$ F.
B. The height of an airplane after taking off from ground level and rising $1,000$ feet.
C. The amount of money received in change after making a $\$10$ purchase with a $\$20$ bill.
D. The distance above sea level after increasing $24$ meters from a depth of [/latex]24[/latex] meters below sea level.

22. Three classes at a junior high raised money to buy new computers.

$\bullet$ Ms. Moore’s class raised $\$249.00$ .
$\bullet$ Ms. Aguilar’s class raised $\$396.62$ more than Ms. Moore’s class.
$\bullet$ Mr. Barry’s class raised $\$430.43$ less than Ms. Aguilar’s class.

What is the total amount raised by all three classes?

A. $\$215.19$
B. $\$464.19$
C. $\$1,076.05$
D. $\$1,109.81$

23. A farm grew $19.8$ tons of wheat in 2013. The farm’s wheat output increased by $9.8\%$ from 2013 to 2014 and by $5.1\%$ from 2014 to 2015. Which expression represents a strategy for estimating the total output of wheat, in tons, in 2015?

A. $20 + 10 + 5$
B. $20(10)(5)$
C. $20 + 1.1 + 1.05$
D. $20(1.1)(1.05)$

26. Lea wants to save money on a new computer. At the store near her, the computer she wants is listed at a regular price of $\$400.00$ .

$\bullet$ On Saturday, the store will have a sale and discount the computer by $30\%$ .
$\bullet$ Shoppers who buy a computer that same Saturday before $9:00$ a.m. will also receive an additional $10\%$ off the sale price.

How much will Lea pay, without tax, when she buys the computer that Saturday before $9:00$ a.m.?

A. $\$148.00$
B. $\$160.00$
C. $\$240.00$
D. $\$252.00$

27. Which expression can go in the blank to make the equation true?
$-4.5 + 4.4 +$ __?__ $= 0$

A. $-6.7 + 6.8$
B. $-6.7 + (-6.6)$
C. $7.2 + (-7.2)$
D. $7.2 + (-7.3)$

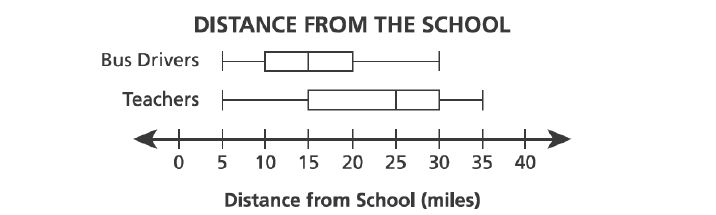
28. A principal gathered data about the distance, in miles, that his teachers and bus drivers live from the school. The box plots below show these data.

Based on the box plots, which statement is true?

A. The interquartile range of the distances for the bus drivers is twice the interquartile range of the distance for the teachers.
B. The range of the distances for the teachers is twice the range of the distances for the bus drivers.
C. The interquartile range of the distance for the bus drivers is $5$ miles less than the interquartile range of the distances for the teachers.
D. The range of the distances for the teachers is $5$ miles less than the range of the distances for the bus drivers.

29. At midnight, the temperature was $-8^{\circ}$ F. At noon, the temperature was $23^{\circ}$ F. Which expression represents the increase in temperature?

A. $-8 - 23$
B. $| -8| - 23$
C. $-8 - |23|$
D. $|-8 - 23|$

30. A spinner with seven equal-sized sections was used to play a game.

$\bullet$ It was used $250$ times in the first game.
$\bullet$ Of those $250$ , the arrow landed on section $7$ a total of $35$ times.
$\bullet$ The same spinner was used $150$ times in the second game.

How many times did the spinner most likely land on section $7$ in the second game?

A. $14$
B. $21$
C. $30$
D. $35$

31. Amanda surveyed $13$ students in her class about their heights in inches. Her data are listed below.
$52, 53, 55, 55, 56, 57, 58, 58, 59, 59, 59, 62, 65$

Which box plot correctly displays her data?

A.
B.
C.
D.

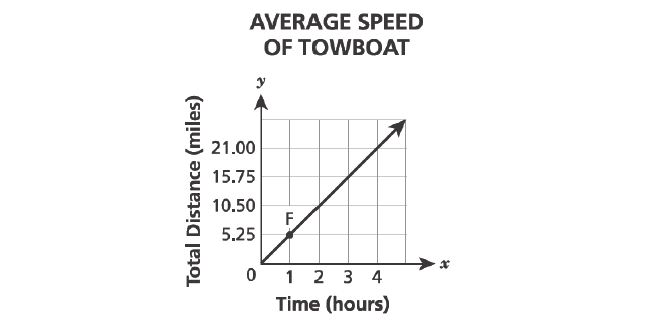
32. The graph below shows the total distance, in miles, traveled by a towboat over time, in hours.

Which statement best describes the meaning of the coordinates of point $F$ on the graph?

A. It shows the unit rate of the graph in hours per mile.
B. It shows the unit rate of the graph in miles per hour.
C. It shows the time, in hours, it takes the towboat to travel $1$ mile.
D. It shows the distance traveled, in miles, by the towboat after $5.25$ hours.

33. A computer program selects blue, red, or green as the background color each time the program is used.

$\bullet$ The program was used $45$ times on the same computer in one week.
$\bullet$ Of those $45$ times, a blue background appeared $12$ times and a red background appeared $21$ times.

Based on this information, which statement about the likelihood of the green background appearing the next time the program is used is true?

A. Green is just as likely as red or blue to appear.
B. Green is just as likely as blue to appear, but not as likely as red.
C. Green is not as likely as red or blue to appear.
D. Green is not as likely as blue to appear but is as likely as red.

34. Which number represents the probability of an event that is very likely to occur?

A. $0.12$
B. $1.3$
C. $0.89$
D. $0.09$

35. Which expression is equivalent to $n + n - 0.18n$ ?

A. $1.18n$
B. $1.82n$
C. $n - 0.18$
D. $2n - 0.82$

36. Nick is making bread dough.

$\bullet$ The recipe requires $\dfrac{3}{4}$ cup of flour and $1\dfrac{1}{8}$ teaspoons of salt.
$\bullet$ Nick wants to make the recipe using $1$ cup of flour.

To maintain the ration, how much salt is required when $1$ cup of flour is used?

A. $\dfrac{27}{32}$ teaspoon
B. $\dfrac{2}{3}$ teaspoon
C. $1\dfrac{1}{2}$ teaspoons
D. $1\dfrac{7}{8}$ teaspoons

37. Which expression is equivalent to $-\dfrac{1}{3}(6x + 15) - 3$ ?

A. $-2x + 12$
B. $-2x + 2$
C. $-2x - 2$
D. $-2x - 8$

38. Josh has a rewards card for a movie theater.

$\bullet$ He receives $15$ points for becoming a rewards card holder.
$\bullet$ He earns $3.5$ points for each visit to the movie theater.
$\bullet$ He needs at least $55$ points to earn a free movie ticket.

Which inequality can Josh use to determine $x$ , the minimum number of visits he needs to earn his first free movie ticket?

A. $55 \geq 3.5x + 15$
B. $55 \geq 15x + 3.5$
C. $55 \leq 3.5x + 15$
D. $55 \leq 15x + 3.5$

39. At a store, a hat has a regular price of $x$ dollars. During a sale, the price of the hat is discounted by $20\%$ . The expression $0.8x$ describes the discounted price, in dollars, of the hat. Which expression also describes the discounted price, in dollars, of the hat?