SAT Math Lesson 4: No Solution/Infinite Solution, Percent, Growth & Decay, Exponents, and Imaginary Numbers

No Solution/Infinite Solutions

The SAT may ask questions regarding two functions that have no solution or infinite solutions.

No Solution to a System of Linear Functions

If you think of the two equations as functions, they would be two functions that never intersect.

If they are both linear equations, they will have the same slope but different y-intercepts.

For example, if we had the system of equations $y=x^2+4$ and $y=2x-3$ , we could graph them and see that they never intersect.

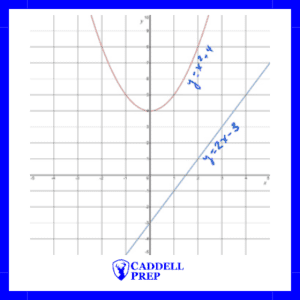
Here is an example of two linear equation that never intersect.

$y=\dfrac{2}{3}x+1$ ,

$3y=2x-6$

It isn’t easy to immediately notice, but both equations have the same slope. Solve for y in the second equation.

$3y=2x-6$

Divide both sides by 3 to get

$y=\dfrac{2}{3}x-2$

Both functions have a slope of $\dfrac{2}{3}$

Here is a graph of both functions.

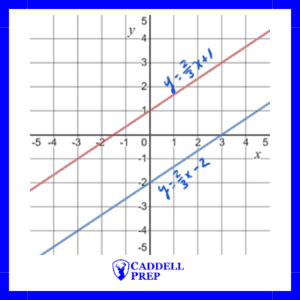
Infinite Solutions to a System of Linear Functions

If you think of the two equations as functions, they would be graphed on top of each other.

If they are both linear equations, they will have the same slope and y-intercept.

For example, the following system of equations has infinite solutions.

$3y-12x=9$ ,

$5y=20x+15$

Solve for y in both equations, and you’ll see that both equations are actually the same: $y=4x+3$ .

If both functions were graphed, they would be graphed right on top of each other, so there would be infinite solutions.

Number of Solutions to Quadratic Equations

If the question asks for the number of real solutions, you may have to use the quadratic formula to see if the solutions are imaginary (not real). Also, if the greatest exponent is 2, it is only possible to have 2, 1 or 0 solutions.

Example

How many solutions are there to the equation $2x^2-4x=9x+1$ ?
A. 3
B. 2
C. 1
D. 0

Explanation & Solution

In this case, you can immediately eliminate choice A, because there can’t be 3 solutions if the greatest exponent is 2.

Since the greatest exponent is 2, we should get one side of the equation equal to zero then see if we can factor. If we can’t factor, use the quadratic formula.

$2x^2-4x=9x+1$

We need to get one side equal to 0, so we can factor or use the quadratic equation.

Subtract 9x from both sides to get

$2x^2-13x=1$

Subtract 1 from both sides to get

$2x^2-13x-1=0$

We can’t factor, so we should use the quadratic equation.

$a=2$ ,

$b=-13$ ,

$c=-1$

Substitute those values into the quadratic equation.

$x=\dfrac{-b+-\sqrt{b^2-4ac}}{2a}$ ,

$x=\dfrac{-(-13)+-\sqrt{(-13)^2-4(2)(-1)}}{2(2)}$ ,

$x=\dfrac{13+-\sqrt{169+4}}{4}$ ,

$x=\dfrac{13+-\sqrt{173}}{4}$ ,

We can stop here. We don’t have to find the exact solutions, just the number of real solutions.

There are two real solutions, they are:

$x=\dfrac{13+\sqrt{173}}{4}$ and $x=\dfrac{13-\sqrt{173}}{4}$

The answer is B. 2

Percent

Students are expected to answer questions on the SAT that incorporate percent. Some questions will be word problems where a student has to find the percent change (percent increase or percent decrease), the new value after a percent increase, or identify an equation that can be used to find a new value after a percent change.

Fractions to Percentages

A percent represents the number you would expect out of 100.

If you are only correct 1 out of every 2 questions, then you would be correct 50 out of 100 times, or 50% of the time.

To change a fraction to a percent, you can create an equivalent fraction with a denominator of 100. The numerator is the percent.

$\dfrac{3}{4}=\dfrac{75}{100}=75%$ ,

$\dfrac{1}{10}=\dfrac{10}{100}=10%$ ,

$\dfrac{2}{5}=\dfrac{40}{100}=40%$

Decimals to Percentages

To change a decimal to a percent, use the fact that $0.38$ means $38$ hundredths, which can be written as $38/100$ ,
and $38/100 = 38%$ .

More simply, to change from a decimal to a percent, move the decimal 2 places right.

$0.45 = 45%$ ,

$0.05 = 5%$ ,

$0.4 =0.40 = 40%$

Percent Formula

$\dfrac{Percent}{100}=\dfrac{Part}{Whole}$

For example, what is 30% of 60?”

$\dfrac{Percent}{100}=\dfrac{Part}{Whole}$

Substitute the values into the equation.

The part is typically associated with “is” in the sentence, and the whole is typically associated with “of” in the sentence.

$\dfrac{30}{100}=\dfrac{x}{60}$

Cross-multiply to get

$1,800=100x$

Divide by sides by 100

$18=x$

Solve by Writing an Equation

In math “of” means multiply and “is” means “equals”.

We can look at the same question and write an equation.

What is 30% of 60

$x=0.30 \times 60$ ,

$x=18$

Tax. Mark-up, & Discount (Increase and Decrease)

Increase by a Percent (Including Tax and Mark-Up)

Tax and mark-up increase the cost of a purchase.

For example, if a pair of shoes is $80 and there is 8% tax, we would have to add the tax on to the total cost.

We would have to calculate the tax and then add it on to the original cost.

8% of $80 is found by multiplying $80 and 0.08.

$.\$80 \times 0.08 = \$6.40$

Now, we have to add the tax on to the price of the shoes,

$\$80+\$6.40=\$86.40$

Solving for the new value in a percent increase in one step (useful algebraic questions)

Another way to look at it is that 100% of the price of the shoes is $80.

If it increases by 8% because of tax, the cost is now 108% of $80.

We can solve for the new total after tax in one step

$\$80 \times 1.08 =\$86.40$ .

The same concept applies to all increases.

If something increases by 40%, it will be 140% of what it previously was.

If something increases by 7.5%, it will be 107.5% of what it previously was.

If something increases by 100%, it will be 200% of what it previously was.

Decrease by a Percent (Including Discount)

Discount decreases the cost of a purchase.

For example, if a pair of shoes is $80 and there is 30% discount, we would have to subtract the discount from the total cost.

We have to calculate the discount and subtract it from the original cost.

30% of $80 is found by multiplying $80 and 0.30.

$\$80 \times 0.30=\$24$ .

Now, we have to subtract the discount from the original cost.

$\$80 - \$24 = \$56$ .

Solving for the new value after a percent decrease in one step (useful for algebraic questions)

Another way to look at it is that 100% of the price of the shoes is $80.

If it decreases by 30% because of tax, the cost is now 70% of $80.

We can solve for the new price after the discount in one step

$\$80 \times 0.70 = \$56$ .

The same concept applies to all decreases.

If something decreases by 40%, it will be 60% of what it previously was.

If something decreases by 7.5%, it will be 92.5% of what it previously was.

If something decreases by 24%, it will be 76% of what it previously was.

Equations that Incorporate Percents

On the SAT, you may be asked to identify equations that can be used to solve for a variable. In other words, sometimes you don’t have to solve for a missing value, you just need to choose the equations that can be used to solve for the missing value.

First, let’s review some expressions.

If a book costs $x and there is 5% tax, the total cost would be $1.05x because we have to increase the cost by 5%.

If a book costs $x and there is 15% discount, the total cost would be $.85x because we have to decrease the cost by 15%, which would leave us with 85% of the cost.

If a book costs $x, but there is a 15% discount and 5% tax, the total cost would be $1.05(.85x).

Percent Change

The formula for percent change, whether increase or decrease, can be found with a simple equation.

Percent Change $= \dfrac{change}{original}\times 100%$

For example, if a stock increased from $80 to $100, the change is $20 and the original value was $80. Let’s use the formula to find the percent change.

Percent Change $= \dfrac{change}{original}\times 100%$
Percent Change $= \dfrac{20}{80}\times 100% = 25%$

If the stock decreased from $100 to $80, the change is still $20, but this time the original value is $100. Let’s use the formula to find the percent change in this scenario.

Percent Change $= \dfrac{change}{original}\times 100%$

Percent Change $= \dfrac{20}{100}\times 100% = 20%$

Growth and Decay

To have a strong understanding of growth and decay for the SAT, you need knowledge of percentages first.

If you haven’t gone through the information on percent, I suggest you go back and review that first.

Exponential Growth

Exponential growth is typically caused by growth that is based on a percentage or ratio. To better understand the difference, compare exponential growth to linear growth. Suppose you deposited $100 in the bank and received $10 every year from the bank for keeping your money there. The amount of money in your account would increase linear because it would increase at a constant rate: $10/year. The amount of money in the account could be represented by the function $f(t)=10t+100$ .

Suppose you deposited $100 in a different bank and received 5% interest each year. The first year you would only receive $5 because 5% of $100 is $5. However, the next year you would receive $5.25 because you would get 5% of $105. The following year, you would receive 5% of $110.25, which is $5.51. The amount of money you receive each year is bigger than the previous year’s amount. This is exponential growth. More precisely, since it is growing by 5%, each year will be 105% of the previous year, so each year will be a multiple of 1.05 of the previous year. The amount of money in the account could be represented by the function $g(t)=100(1.05)^t$ .

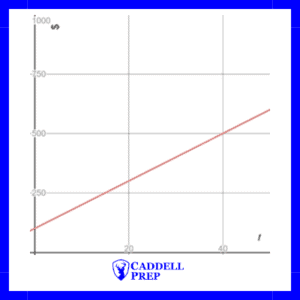
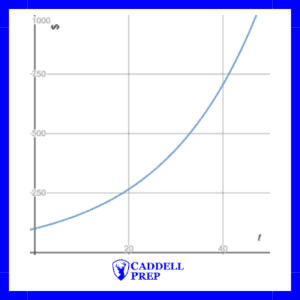
Here is a comparison of the two. As you can see from the graph, exponential growth results in a graph that is curved upward.

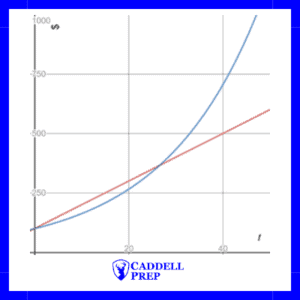
The function $g(t)=100(1.05)^t$ is based on an initial value of $100 that increases by 5% each year. It is based on the general formula:

$A=A_0 (1+r)^t$

where $A$ is the value, $A_0$ is the initial value (in this case $100), $r$ is the rate (in this case .05 for 5%), and $t$ is time (in this case in years)

Since we add the rate to 1, we end up with growth.

Exponential Decay

Like exponential growth, exponential decay is typically based on a percentage or ratio. However, since it is decaying (decreasing) the ratio is less than one. Let’s look at an example. Suppose the population of an organism was initially 10,000 and the population decreases by 5% each year. The first year, the population would decrease by 5% of 10,000, which is 500. The population next year would start at 9,500 and would decrease by 5% again that year, so it would decrease by 475. Each year, the population decreases by 5%. More precisely, since it is decreasing by 5%, each year will be 95% of the previous year, so each year will be a multiple of 0.95 of the previous year. The population of the organisms could be represented by the function $P(t)=10,000(0.95)^t$ . Here is a graph of $P(t)$ .

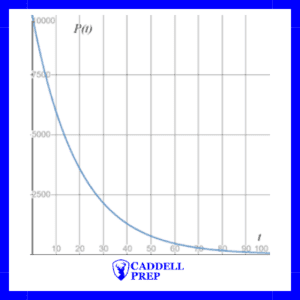
The function $P(t)=10,000(0.95)^t$ is based on an initial value of 10,000 that decreases by 5% each year. It is based on the general formula:

$A=A_0 (1-r)^t$
where $A$ is the value, $A_0$ is the initial value (in this case 10,000), $r$ is the rate (in this case .05 for 5%), and $t$ is time (in this case in years)

Since we subtract the rate from 1, we end up with decay.

Exponents

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.

Multiplying Terms with Exponents

When you multiply terms that have the same base, you add exponents.

$x^2\times x^5=x^7$

Here is a more complicated one

$x^2 y^3 z \times xy^5 z^4$

If there is no exponent written, there is an exponent of 1.

Dividing Terms with Exponents

When you divide terms that have the same base, you subtract exponents.

$\dfrac{x^8}{x^3}=x^5$
x^8/x^3 =x^5

Here is a more complicated one

$\dfrac{x^5 y^3 z^4}{x^2y^3z}$

The y^3 terms in the numerator and denominator cancel out. The other exponents subtract.

$x^3z^3$

Raising an Expression with an Exponent to an Exponent

When you raise an expression with exponents to another power, you multiply the exponents.

Example

Simplify the expression below.

$(a^3 b^2 c^8 )^3$

becomes

$a^9b^6c^24$

Exponent of Zero

Any number raised to zero is 1.

$x^0=1$

Also

$(\dfrac{x^2 y^3-32}{4x^5-3z^2 })^0=1$

There are a lot of terms, but the entire expression is raised to 0, so it is equal to 1.

Be careful.

$xy^0=x(1)=x$

In this example, only the $y$ is raised to 0, so $y^0$ becomes 1. The $x$ remains $x$ .

Negative Exponents

Think of a negative exponent as a sign that the term is in the wrong spot. If it is in the numerator, move it to the denominator and make the exponent positive. If it is in the denominator, move it to the numerator and make it negative.

For example

$\dfrac{x^2 y^3}{a^{-4} b^2 }$

In the example above, the exponent for the a is negative, so move it to the numerator.

$\dfrac{a^4 x^2 y^3}{b^2}$

Here is another example

$\dfrac{2x^{-4} y^2}{z^3}$

Only the $x$ has a negative exponent, so only the $x$ should move to the denominator with its exponent. Do not move the coefficient, 2.

Moving the 2 along with the $x$ is a common mistake.

We would end up with
$\dfrac{2y^2}{x^4 z^3}$

Fractions as Exponents

A fraction in the exponent represents a root, such as a square root or cubed root.

$x^{\frac{1}{2}}=\sqrt{x}$ ,

$x^{\frac{1}{3}}=\sqrt[3]{x}$ ,

$x^{\frac{1}{4}}=\sqrt[4]{x}$

The denominator of the exponent represents the root.

It is possible for the numerator to be a number other than 1. Treat the numerator like a regular exponent.

$x^{\frac{4}{3}}=\sqrt[3]{x^4}$

The 4 in the numerator means to the 4th power. The 3 in the denominator means cubed root.

Example

Rewrite $x^{\frac{5}{2}}/$ with an integer power and root.

Explanation & Solution

5 is the power, and 2 is the root

$x^{\frac{5}{2}}=\sqrt{x^5}$

Imaginary Numbers

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.

Imaginary Number, i

$\sqrt{-1}$ does not result in a real number. There is no real number that when multiplied by itself will result in $-1$ .

$\sqrt{-1}$ is imaginary. We represent this imaginary number with the letter $i$ .

$\sqrt{-1}=i$

Combining Like Terms

When combining like terms, treat $i$ as if it’s a variable.

For example, $3$ and $3i$ are not like terms but $12i$ and – $3i$ are, just like $3$ and $3x$ are not like terms, but $12x$ and $-3x$ are.

When combining like terms, just add the coefficients.

A simplified expression is typically in $a+bi$ form, where the number is written first followed by the $i$ -term.

Example

Simplify $3+2i-8i+7$ .

Explanation & Solution

Here we will combine like terms by adding the like terms together.

$3$ and $7$ are like terms, so we can add them together to get $10$ . $2i$ and $-8i$ are like terms, so we can add them together to get $-6i$ .

We end up with $3-6i$ , which is in $a+bi$ form. In this case, $a$ is $3$ and $b$ is $-6$ .

Multiplying and Simplifying Complex Expressions

Since $\sqrt{-1}=i$ , then $i^2=-1$ .

When we multiply terms or expressions that have $i$ , we may end up with terms that have $i^2$ .

It’s important to remember that $i^2$ is simply $-1$ .

Example

Simplify $(2-5i)(3+2i)$ .

Explanation & Solution

To simplify this, we will have to distribute twice (FOIL).

$2\times 3=6$ ,

$2\times2 i=4i$ ,

$-5i\times 3=-15i$ ,

$-5i\times 2i=-10i^2$

So we would end up with

$6+4i-15i-10i^2$

We an combine the like terms,

$4i$ and $15i$ , to get

$6-11i-10i^2$

Remember that $i^2$ is really

$-1$ , so we have

$6-11i-10(-1)$ ,

$6-11i+10$

Now, we can combine like terms to get

$16-11i$ .

Rationalizing the Denominator When the Denominator has an i-term

Occasionally on the SAT, you may see a question that requires rationalizing the denominator.

In this case, the denominator has an expression including $i$ .

To rationalize the following, we would simply multiply the number and denominator by $i$ .

$\dfrac{3+2i}{4i}$ ,

$\dfrac{i(3+2i}{i(4i)}$ ,

$\dfrac{3i+2i^2}{4i^2}$ ,

Remember that $i^2$ is

$-1$ ,

$(3i+2(-1))/(4(-1))$ ,

$(3i-2)/(-4)$

We typically wouldn’t write a negative number in the denominator, so we should negate the numerator and denominator.

Our final answer is

$(-3i+2)/4$ ,

If we have to write it in $a+bi$ form, we would divide both terms in the numerator by the denominator to get

$\dfrac{-3}{4} i+\dfrac{1}{2}$

And write the $i$ -term second
$\dfrac{1}{2}-\dfrac{3}{4} i$

Table of Contents

No Solution/Infinite Solutions

No Solution to a System of Linear Functions

Infinite Solutions to a System of Linear Functions

Number of Solutions to Quadratic Equations

Percent

Fractions to Percentages

Decimals to Percentages

Percent Formula

Tax. Mark-up, & Discount (Increase and Decrease)

Increase by a Percent (Including Tax and Mark-Up)

Decrease by a Percent (Including Discount)

Equations that Incorporate Percents

Percent Change

Growth and Decay

Exponential Growth

Exponential Decay

Exponents

Multiplying Terms with Exponents

Dividing Terms with Exponents

Raising an Expression with an Exponent to an Exponent

Exponent of Zero

Negative Exponents

Fractions as Exponents

Imaginary Numbers

Imaginary Number, i

Combining Like Terms

Multiplying and Simplifying Complex Expressions

Rationalizing the Denominator When the Denominator has an i-term