Learn Midpoint Formula, How to Find the Midpoint Using Coordinates

In this video, you will learn the midpoint formula and how to use the midpoint formula to calculate the midpoint of a line segment if the two endpoints are known. Also, you will learn how to calculate the coordinates of an endpoint if the midpoint and the other endpoint is given. After you finish this lesson, view all of our Pre-Algebra lessons and practice problems.

What is the midpoint formula?

The midpoint formula is based on the average of the x-coordinates and the average of the y-coordinates. The formula is used to find the coordinates of the midpoint of a line segment in the x-y plane.

Midpoint Formula: $(X,Y)=(\frac{X_1 + X_2}{2}, \frac{Y_1 + Y_2}{2})$
In other words, we are simply finding the average of the two x-values and the two y-values.

To better understand how to apply the formula, let’s take a look at a couple of midpoint formula problems.

For example:
Given points $A(1,5)$ and $B(7,3)$ , find the midpoint.

By using the midpoint formula, substitute each value into the formulahttps://caddellprep.com/subjects/common-core-geometry/midpoint-formula/?preview=true
$(X,Y)=(\frac{X_1 + X_2}{2}, \frac{Y_1 + Y_2}{2})$
$(X,Y)=(\frac{1+7}{2}, \frac{5+3}{2})$

Combine like terms
$(X,Y)=(\frac{8}{2}, \frac{8}{2})$

Divide each expression
$(X,Y)=(4, 4)$

Let’s try an example where only one endpoint and the midpoint is given. In this problem we will find the other endpoint.

For example:
$M$ is the midpoint of $\overline{AB}$ . The coordinates of $B$ are $(4,-3)$ and the coordinates of $M$ are $(-3,-1)$ . Find the coordinates of $A$ .

Like the previous example, substitute the x and the y-values.
$(X,Y)=(\frac{X_1 + X_2}{2}, \frac{Y_1 + Y_2}{2})$
$(-3,-1)=(\frac{4 + X}{2}, \frac{-3 + Y}{2})$

Separate the equation to solve for x and y individually
x
$-3 =\frac{4 + X}{2}$
$-6 = 4 + x$
$-10 = x$

y
$-1=\frac{-3 + Y}{2}$
$-2 = -3 + y$
$1 = y$

Examples of Midpoint Formula

Example 1

Find the midpoint of the two points $A(1, -3)$ and $B(4, 5)$ .

First, substitute each value into the formula

$(X,Y)=(\dfrac{X_1 + X_2}{2}, \dfrac{Y_1 + Y_2}{2})$

$(X,Y)=(\dfrac{1+4}{2}, \dfrac{-3+5}{2})$

Then, combine like terms

$(X,Y)=(\dfrac{5}{2}, \dfrac{2}{2})$

Lastly, divide each expression

$(X,Y)=(2.5, 1)$

Example 2

Find the missing value of y in the points $(5, 7)$ and $(1, y)$ if its midpoint is at $(3,{-}2)$ .

First, substitute each value into the formula

$(X,Y)=(\dfrac{X_1 + X_2}{2}, \dfrac{Y_1 + Y_2}{2})$

$(3,-2)=(\dfrac{5+1}{2}, \dfrac{7+y}{2})$

Then, let’s solve for $y$ since it is the missing value

$-2=\dfrac{7+y}{2}$

$-4=7+y$

$-11=y$

Video-Lesson Transcript

Let’s go over the midpoint formula.

We have two points – $A$ and $B$ in the $XY$ -system.

The midpoint is the point in the middle of these two points.

Remember, $A$ and $B$ is a line segment each with corresponding $x$ and $y$ coordinates. So the midpoint also has $x$ and $y$ coordinates.

Let’s call the coordinates of $A$ as $x_1$ and $y_1$ . Likewise, $B$ coordinates are $x_2$ and $y_2$ .

The midpoint has the same distance not only between $A$ and $B$ but also between the two $x$ -coordinates and $y$ -coordinates.

Let’s call the midpoint coordinates as $x_m$ and $y_m$ . Midpoint coordinates are the average of the two coordinates.

So our formula is:

$\big( \dfrac{(x_1 + x_2)}{2} , \dfrac{(y_1 + y_2)}{2} \big)$

For example:

Let’s find the midpoint of a line segment which has point $A$ with coordinates $(1, 5)$ and point $B$ with $(7, 3)$ coordinates.

Let’s use our formula – average of the two $X$ coordinates and the two $Y$ coordinates.

$\big( \dfrac{(x_1 + x_2)}{2} , \dfrac{(y_1 + y_2)}{2} \big)$

Let’s label the coordinates first so we won’t be confused.

Then substitute the given

$\big( \dfrac{(1 + 7)}{2} , \dfrac{(5 + 3)}{2} \big)$

$1 + 7 = 8 \div 2 = 4$

$5 + 3 = 8 \div 2 = 4$

So our midpoint is $(4, 4)$

The midpoint of the line segment from point A to point B is found by taking the average of the x-coordinates and the average of the y-coordinates

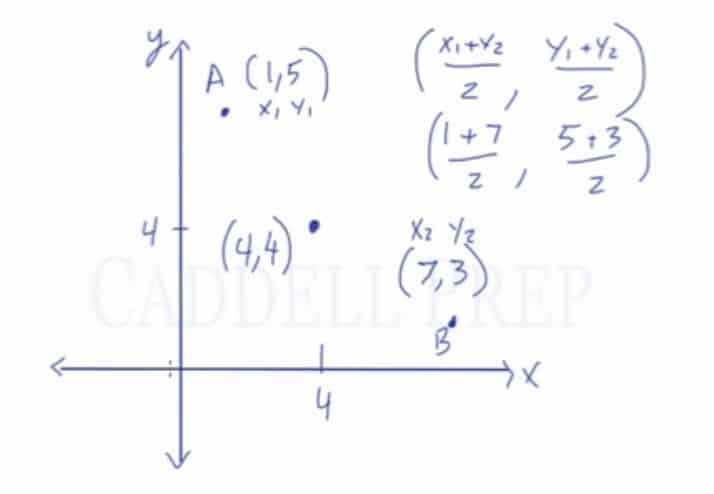
This is just a coincidence that we came up with an identical value. But we can come up with any value for the $x$ – and $y$ -coordinates.

Just follow the formula.