June 2015 Geometry Regents

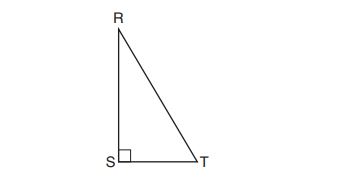
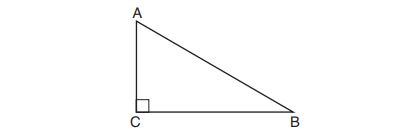
1. Which object is formed when right triangle $RST$ shown below is rotated around leg $\overline{RS}$ ?

(1) a pyramid with a square base
(2) an isosceles triangle
(3) a right triangle
(4) a cone

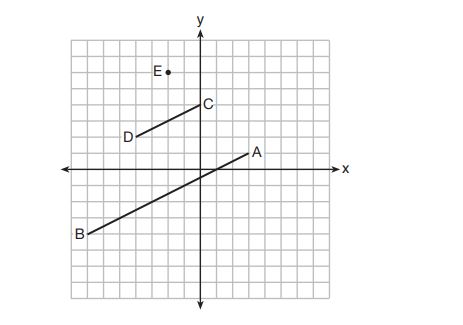
2. The vertices of $\triangle JKL$ have coordinates $J (5, 1)$ , $K (-2, -3)$ , and $L (-4, 1)$ . Under which transformation is the image $\triangle J'K'L'$ not congruent to $\triangle JKL$ ?

(1) a translation of two units to the right and two units down
(2) a counterclockwise rotation of $180$ degrees around the origin
(3) a reflection over the $x-axis$
(4) a dilation with a scale factor of $2$ and centered at the origin

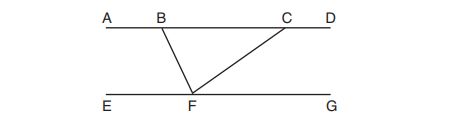
3. The center of circle $Q$ has coordinates ( $3, 2$ ). If circle $Q$ passes through $R (7, 1)$ , what is the length of its diameter?

(1) $50$
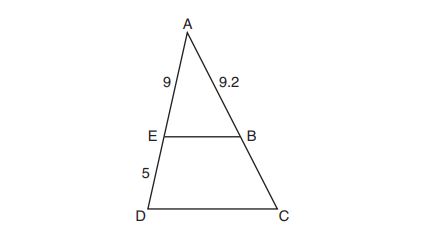
(2) $25$
(3) $10$
(4) $5$

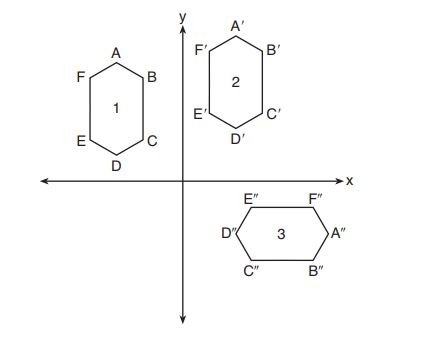
4. In the diagram below, congruent figures 1, 2, and 3 are drawn.

Which sequence of transformations maps figure 1 onto figure 2 and then figure 2 onto figure 3?

(1) a reflection followed by a translation
(2) a rotation followed by a translation
(3) a translation followed by a reflection
(4) a translation followed by a rotation

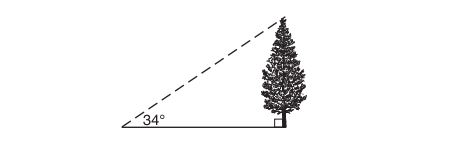
5. As shown in the diagram below, the angle of elevation from a point on the ground to the top of the tree is $34^{\circ}$ .

If the point is 20 feet from the base of the tree, what is the height of the tree, to the nearest tenth of a foot?

(1) $29.7$
(2) $16.6$
(3) $13.5$
(4) $11.2$

6. Which figure can have the same cross section as a sphere?

7. A shipping container is in the shape of a right rectangular prism with a length of $12$ feet, a width of $8.5$ feet, and a height of $4$ feet. The container is completely filled with contents that weigh, on average, $0.25$ pound per cubic foot.
What is the weight, in pounds, of the contents in the container?

(1) $1,632$
(2) $408$
(3) $102$
(4) $92$

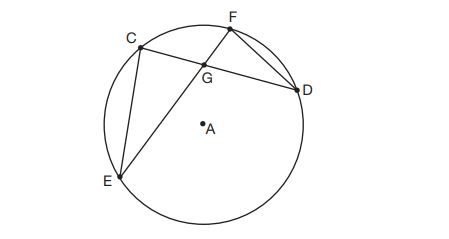
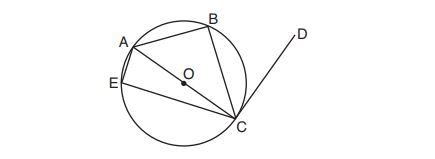
8. In the diagram of circle $A$ shown below, chords $\overline{CD}$ and $\overline{EF}$ intersect at $G$ , and chords $\overline{CE}$ and $\overline{FD}$ are drawn.

Which statement is not always true?

(1) $\overline{CG} \cong \overline{FG}$
(2) $\angle CEG \cong \angle FDG$
(3) $\dfrac{CE}{EG} = \dfrac{FD}{DG}$
(4) $\triangle CEG \sim \triangle FDG$

9. Which equation represents a line that is perpendicular to the line represented by $2x - y = 7$ ?

(1) $y = -\dfrac{1}{2}x + 6$
(2) $y = \dfrac{1}{2}x + 6$
(3) $y = -2x + 6$
(4) $y = 2x + 6$

10. Which regular polygon has a minimum rotation of $45^{\circ}$ to carry the polygon onto itself?

(1) octagon
(2) decagon
(3) hexagon
(4) pentagon

11. In the diagram of $\triangle ADC$ below, $\overline{EB} \| \overline{DC} , AE = 9, ED = 5$ , and $AB = 9.2$ .

What is the length of $\overline{AC}$ , to the nearest tenth?

(1) $5.1$
(2) $5.2$
(3) $14.3$
(4) $14.4$

12. In scalene triangle $ABC$ shown in the diagram below, $m \angle C = 90^{\circ}$ .

Which equation is always true?

(1) $sin A = sin B$
(2) $cos A = cos B$
(3) $cos A = sin C$
(4) $sin A = cos B$

13. Quadrilateral $ABCD$ has diagonals $\overline{AC}$ and $\overline{BD}$ . Which information is not sufficient to prove $ABCD$ is a parallelogram?

(1) $\overline{AC}$ and $\overline{BD}$ bisect each other
(2) $\overline{AB} \cong \overline{CD}$ and $\overline{BC} \cong \overline{AD}$
(3) $\overline{AB} \cong \overline{CD}$ and $\overline{AB} \| \overline{CD}$
(4) $\overline{AB} \cong \overline{CD}$ and $\overline{BC} \| \overline{AD}$

14. The equation of a circle is $x^{2} + y^{2} + 6y = 7$ . What are the coordinates of the center and the length of the radius of the circle?

(1) center ( $0, 3$ ) and radius $4$
(2) center ( $0, -3$ ) and radius $4$
(3) center ( $0, 3$ ) and radius $16$
(4) center ( $0, -3$ ) and radius $16$

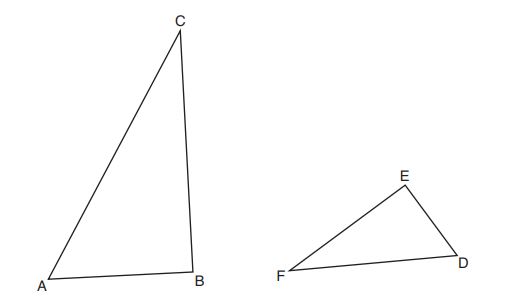
15. Triangles $ABC$ and $DEF$ are drawn below.

If $AB = 9, BC = 15, DE = 6, EF = 10,$ and $\angle B \cong \angle E$ , which statement is true?

(1) $\angle CAB \cong \angle DEF$
(2) $\dfrac{AB}{CB} = \dfrac{FE}{DE}$
(3) $\triangle ABC \sim \triangle DEF$
(4) $\dfrac{AB}{DE} = \dfrac{FE}{CB}$

15. If $\triangle ABC$ is dilated by a scale factor of $3$ , which statement is true of the image $\triangle A'B'C'$ ?

(1) $3A'B' = AB$
(2) $B'C' = 3BC$
(3) $m\angle A' = 3(m\angle A)$
(4) $3(m\angle C') = m\angle C$

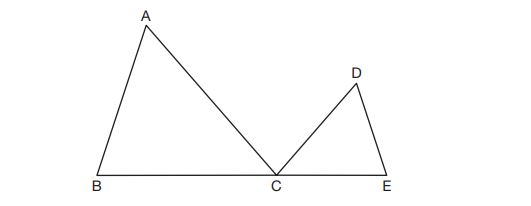
17. Steve drew line segments $ABCD, EFG, BF,$ and $CF$ as shown in the diagram below. Scalene $\triangle BFC$ is formed.

Which statement will allow Steve to prove $\overline{ABCD} \| \overline{EFG}$ ?

(1) $\angle CFG \cong \angle FCB$
(2) $\angle ABF \cong \angle BFC$
(3) $\angle EFB \cong \angle CFB$
(4) $\angle CBF \cong \angle GFC$

18. In the diagram below, $\overline{CD}$ is the image of $\overline{AB}$ after a dilation of scale factor $k$ with center $E$ .

Which ratio is equal to the scale factor $k$ of the dilation?

(1) $\dfrac{EC}{EA}$
(2) $\dfrac{BA}{EA}$
(3) $\dfrac{EA}{BA}$
(4) $\dfrac{EA}{EC}$

19. A gallon of paint will cover approximately $450$ square feet. An artist wants to paint all the outside surfaces of a cube measuring $12$ feet on each edge. What is the least number of gallons of paint he must buy to paint the cube?

(1) $1$
(2) $2$
(3) $3$
(4) $4$

20. In circle $O$ shown below, diameter $\overline{AC}$ is perpendicular to $\overline{CD}$ at point $C$ , and chords $\overline{AB}$ , $\overline{BC}$ , $\overline{AE}$ , and $\overline{CE}$ are drawn.

Which statement is not always true?

(1) $\angle ACB \cong \angle BCD$
(2) $\angle ABC \cong \angle ACD$
(3) $\angle BAC \cong \angle DCB$
(4) $\angle CBA \cong \angle AEC$

21. In the diagram below, $\triangle ABC \sim \triangle DEC$ .

If $AC = 12$ , $DC = 7$ , $DE = 5$ , and the perimeter of $\triangle ABC$ is $30$ , what is the perimeter of $\triangle DEC$ ?

(1) $12.5$
(2) $14.0$
(3) $14.8$
(4) $17.5$

22. The line $3y = -2x + 8$ is transformed by a dilation centered at the origin. Which linear equation could be its image?

(1) $2x + 3y = 5$
(2) $2x - 3y = 5$
(3) $3x + 2y = 5$
(4) $3x - 2y = 5$

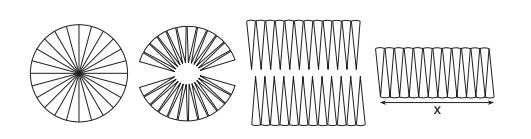
23. A circle with a radius of $5$ was divided into $24$ congruent sectors. The sectors were then rearranged, as shown in the diagram below.

To the nearest integer, the value of $x$ is

(1) $31$
(2) $16$
(3) $12$
(4) $10$

24. Which statement is sufficient evidence that $\triangle DEF$ is congruent to $\triangle ABC$ ?

(1) $AB = DE$ and $BC = EF$
(2) $\angle D \cong \angle A, \angle B \cong \angle E, \angle C \cong \angle F$
(3) There is a sequence of rigid motions that maps $\overline{AB}$ onto $\overline{DE}$ , $\overline{BC}$ onto $\overline{EF}$ , and $\overline{AC}$ onto $\overline{DF}$
(4) There is a sequence of rigid motions that maps point $A$ onto point $D$ , $\overline{AB}$ onto $\overline{DE}$ , and $\angle B$ onto $\angle E$ .