January 2018 Algebra One Regents

Answer all 24 questions in this part. Each correct answer will receive 2 credits. No partial credit will be allowed. Utilize the information provided for each question to determine your answer. Note that diagrams are not necessarily drawn to scale. For each statement or question,
choose the word or expression that, of those given, best completes the statement or answers the question. Record your answers on your separate answer sheet.

Part I – Multiple Choice

1. When solving the equation $12x^{2} - 7x = 6 - 2(x^{2} - 1)$ , Evan wrote $12x^{2} - 7x = 6 - 2x^{2} + 2$ as his first step. Which property justifies this step?

(1) subtraction property of equality
(2) multiplication property of equality
(3) associative property of multiplication
(4) distributive property of multiplication over subtraction

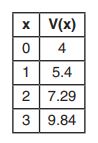
2. Jill invests $\$400/$ in a savings bond. The value of the bond, $V(x)$ , in hundreds of dollars after $x$ years is illustrated in the table below.

Which equation and statement illustrate the approximate value of the bond in hundreds of dollars over time in years?

(1) $V(x) = 4(0.65)^{x}$ , and it grows.
(2) $V(x) = 4(0.65)^{x}$ , and it decays.
(3) $V(x) = 4(1.35)^{x}$ , and it grows.
(4) $V(x) = 4(1.35)^{x}$ , and it decays.

3. Alicia purchased $H$ half-gallons of ice cream for $\$3.50$ each and $P$ packages of ice cream cones for $\$2.50$ each. She purchased $14$ items and spent $\$43$ . Which system of equations could be used to determine how many of each item Alicia purchased?

(1) $3.50H + 2.50P = 43$ ,
$H + P = 14$

(2) $3.50P + 2.50H = 43$ ,
$P + H = 14$

(3) $3.50H + 2.50P = 14$ ,
$H + P = 43$

(4) $3.50P + 2.50H = 14$ ,
$P + H = 43$

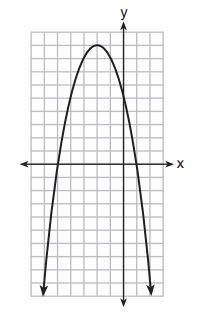
4. A relation is graphed on the set of axes below.

Based on this graph, the relation is

(1) a function because it passes the horizontal line test
(2) a function because it passes the vertical line test
(3) not a function because it fails the horizontal line test
(4) not a function because it fails the vertical line test

5. Ian is saving up to buy a new baseball glove. Every month he puts $\$10$ into a jar. Which type of function best models the total amount of money in the jar after a given number of months?

(1) linear
(2) exponential
(3) quadratic
(4) square root

6. Which ordered pair would not be a solution to $y = x^{3} - x$ ?

(1) $(-4, -60)$
(2) $(-3, -24)$
(3) $(-2, -6)$
(4) $(-1, -2)$

7. Last weekend, Emma sold lemonade at a yard sale. The function $P(c) = .50c - 9.96$ represented the profit, $P(c)$ , Emma earned selling $c$ cups of lemonade. Sales were strong, so she raised the price for this weekend by $25$ cents per cup. Which function represents her profit for this weekend?

(1) $P(c) = .25c - 9.96$
(2) $P(c) = .50c - 9.71$
(3) $P(c) = .50c - 10.21$
(4) $P(c) = .75c - 9.96$

8. The product of $\sqrt{576}$ and $\sqrt{684}$ is

(1) irrational because both factors are irrational
(2) rational because both factors are rational
(3) irrational because one factor is irrational
(4) rational because one factor is rational

9. Which expression is equivalent to $y^{4} - 100$ ?

(1) $(y^{2} - 10)^{2}$
(2) $(y^{2} - 50)^{2}$
(3) $(y^{2} + 10) (y^{2} - 10)$
(4) $(y^{2} + 50) (y^{2} - 50)$

10. The graphs of $y = x^{2} - 3$ and $y = 3x - 4$ intersect at approximately

(1) $(0.38, -2.85)$ only
(2) $(2.62, 3.85)$ only
(3) $(0.38, -2.85)$ and $(2.62, 3.85)$
(4) $(0.38, -2.85)$ and $(3.85, 2.62)$

11. The expression $-4.9t^{2} + 50t + 2$ represents the height, in meters, of a toy rocket t seconds after launch. The initial height of the rocket, in meters, is

(1) $0$
(2) $2$
(3) $4.9$
(4) $50$

12. If the domain of the function $f(x) = 1x^{2} - 8$ is { $-2, 3, 5$ }, then the range is

(1) { $-16, 4, 92$ }
(2) { $-16, 10, 42$ }
(3) { $0, 10, 42$ }
(4) { $0, 4, 92$ }

13. Which polynomial is twice the sum of $4x^{2} - x + 1$ and $-6x^{2} + x - 4$ ?

(1) $-2x^{2} - 3$
(2) $-4x^{2} - 3$
(3) $-4x^{2} - 6$
(4) $-2x^{2} +x - 5$

14. What are the solutions to the equation $-3 (x - 4)^{2} = 27$ ?

(1) $1$ and $7$
(2) $-1$ and $-7$
(3) $4 \pm \sqrt{24}$
(4) $-4 \pm \sqrt{24}$

15. A system of equations is shown below.

Equation A: $5x + 9y = 12$
Equation B: $4x - 3y = 8$

Which method eliminates one of the variables?

(1) Multiply equation $A$ by $-\dfrac{1}{3}$ and add the result to equation $B$ .
(2) Multiply equation $B$ by $3$ and add the result to equation $A$ .
(3) Multiply equation $A$ by $2$ and equation $B$ by $26$ and add the results together.
(4) Multiply equation $B$ by $5$ and equation $A$ by $4$ and add the results together.

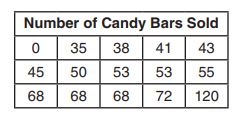
16. The $15$ members of the French Club sold candy bars to help fund their trip to Quebec. The table below shows the number of candy bars each member sold.

When referring to the data, which statement is false?

(1) The mode is the best measure of central tendency for the data.
(2) The data have two outliers.
(3) The median is $53$ .
(4) The range is $120$ .

17. Given the set { $x| -2 \leq x \leq 2$ , where $x$ is an integer}, what is the solution of $-2 (x - 5) \textless 10$ ?

(1) $0, 1, 2$
(2) $1, 2$
(3) $-2, -1, 0$
(4) $-2, -1$

18. If the pattern below continues, which equation(s) is a recursive formula that represents the number of squares in this sequence?

(1) $y = 2x + 1$
(2) $y = 2x + 3$
(3) $a_1 = 3$ ,
$a_n = a_{n-1} + 2$
(4) $a_1 = 1$ ,
$a_n = a_{n - 1} + 2$

19. If the original function $f(x) = 2x^{2} - 1$ is shifted to the left $3$ units to make the function $g(x)$ , which expression would represent $g(x)$ ?

(1) $2(x - 3)^{2} - 1$
(2) $2(x + 3)^{2} - 1$
(3) $2x^{2} + 2$
(4) $2x^{2} - 4$

20. First consider the system of equations $-\dfrac{1}{2}x + 1$ and $y = x - 5$ .

Then consider the system of inequalities $y \textgreater -\dfrac{1}{2}x + 1$ and $y \textless x - 5$ .

When comparing the number of solutions in each of these systems, which statement is true?

(1) Both systems have an infinite number of solutions.
(2) The system of equations has more solutions.
(3) The system of inequalities has more solutions.
(4) Both systems have only one solution.

21. Nora inherited a savings account that was started by her grandmother $25$ years ago. This scenario is modeled by the function
$A(t) = 5000(1.013)^{t + 25}$ , where $A(t)$ represents the value of the account, in dollars, $t$ years after the inheritance. Which function below is equivalent to $A(t)$ ?

(1) $A(t) = 5000 [ (1.013^{t})]^{25}$
(2) $A(t) = 5000 [ (1.013)^{t} + (1.013)^{25}]$
(3) $A(t) = (5000)^{t} (1.013)^{25}$
(4) $A(t) = 5000 (1.013)^{t} (1.013)^{25}$

22. The value of $x$ which makes $\dfrac{2}{3} (\dfrac{1}{4}x -2) = \dfrac{1}{5} (\dfrac{4}{3}x -1)$ true is

(1) $-10$
(2) $-2$
(3) $-9.\overline{09}$
(4) $-11.\overline{3}$

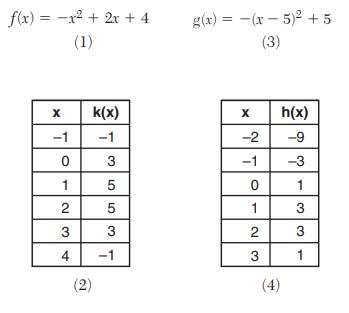
23. Which quadratic function has the largest maximum over the set of real numbers?

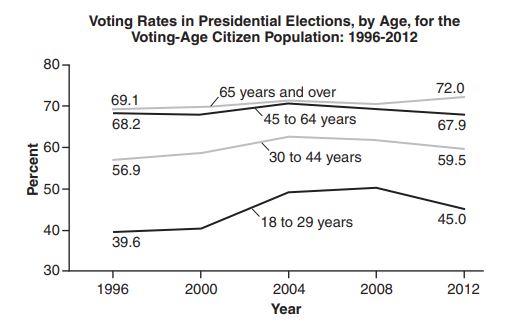
24. Voting rates in presidential elections from 1996-2012 are modeled below.

Which statement does not correctly interpret voting rates by age based on the given graph?

(1) For citizens 18-29 years of age, the rate of change in voting rate was greatest between years 2000-2004.
(2) From 1996-2012, the average rate of change was positive for only two age groups.
(3) About $70\%$ of people $45$ and older voted in the 2004 election.
(4) The voting rates of eligible age groups lies between $35$ and $75$ percent during presidential elections every $4$ years from 1996-2012.

January 2018 Algebra One Regents

Want access to the rest of the test with video explanations?

Go to our Algebra Regents Course for lessons, practice problems, and more sample tests

Part I – Multiple Choice