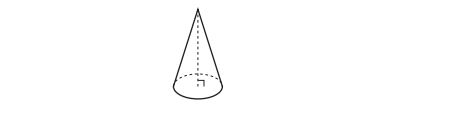
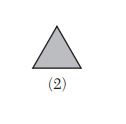
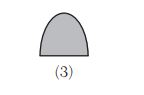
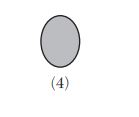
1. William is drawing pictures of cross sections of the right circular cone below.
Which drawing can not be a cross section of a cone?
2. An equation of a line perpendicular to the line represented by the equation and passing through (
) is
(1)
(2)
(3)
(4)
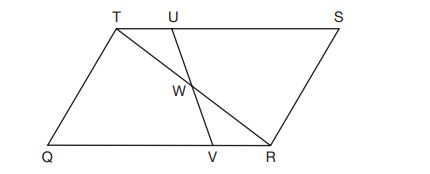
3. In parallelogram shown below, diagonal
is drawn,
and
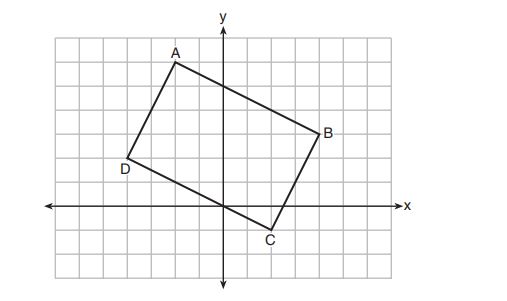
are points on
and
, respectively, and
intersects
at
.
If , and
, what is
?
(1)
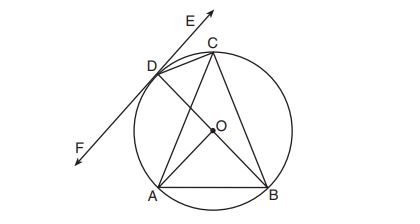
(2)
(3)
(4)
4. A fish tank in the shape of a rectangular prism has dimensions of inches,
inches, and
inches. The tank contains
cubic inches of water. What percent of the fish tank is empty?
(1)
(2)
(3)
(4)
5. Which transformation would result in the perimeter of a triangle being different from the perimeter of its image?
(1)
(2)
(3)
(4)
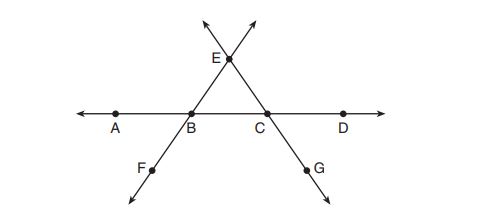
6. In the diagram below, bisects
at
, and
bisects
at
.
Which statement is always true?
(1)
(2)
(3) bisects
at
(4) bisects
at
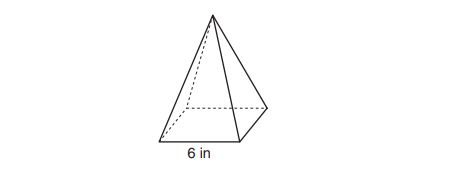
7. As shown in the diagram below, a regular pyramid has a square base whose side measures inches.
If the altitude of the pyramid measures inches, its volume, in cubic inches, is
(1)
(2)
(3)
(4)
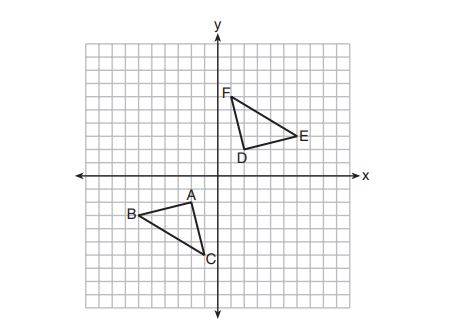
8. Triangle and triangle
are graphed on the set of axes below.
Which sequence of transformations maps triangle onto triangle
?
(1) a reflection over the -axis followed by a reflection over the
-axis
(2) a rotation about the origin followed by a reflection over the line
(3) a clockwise rotation about the origin followed by a reflection over the
-axis
(4) a translation units to the right and
unit up followed by a
counterclockwise rotation about the origin
9. In , the complement of
is
. Which statement is always true?
(1)
(2)
(3)
(4)
10. A line that passes through the points whose coordinates are () and (
) is dilated by a scale factor of
and centered at the origin. The image of the line
(1) is perpendicular to the original line
(2) is parallel to the original line
(3) passes through the origin
(4) is the original line
11. Quadrilateral is graphed on the set of axes below.
When is rotated
in a counterclockwise direction about the origin, its image is quadrilateral
. Is distance preserved
under this rotation, and which coordinates are correct for the given vertex?
(1) no and
(2) no and
(3) yes and
(4) yes and
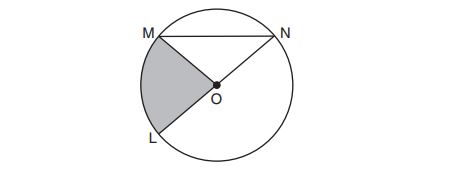
12. In the diagram below of circle , the area of the shaded sector
is
.
If the length of is
cm, what is
?
(1)
(2)
(3)
(4)
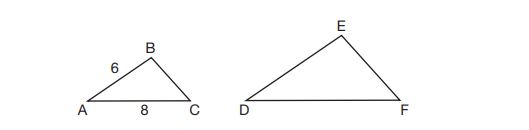
13. In the diagram below, .
If and
, which statement will justify similarity by SAS?
(1) and
(2) and
(3) and
(4) and
14. The diameter of a basketball is approximately inches and the diameter of a tennis ball is approximately
inches. The volume of the basketball is about how many times greater than the volume of the tennis ball?
(1)
(2)
(3)
(4)
15. The endpoints of one side of a regular pentagon are () and (
). What is the perimeter of the pentagon?
(1)
(2)
(3)
(4)
16. In the diagram of right triangle shown below,
and
.
What is the measure of , to the nearest degree?
(1)
(2)
(3)
(4)
17. What are the coordinates of the center and length of the radius of the circle whose equation is ?
(1) () and
(2) () and
(3) () and
(4) () and
18. The coordinates of the vertices of are
, and
. Which type of triangle is
?
(1) right
(2) acute
(3) obtuse
(4) equiangular
19. Molly wishes to make a lawn ornament in the form of a solid sphere. The clay being used to make the sphere weighs pound per cubic inch. If the sphere’s radius is
inches, what is the weight of the sphere, to the nearest pound?
(1)
(2)
(3)
(4)
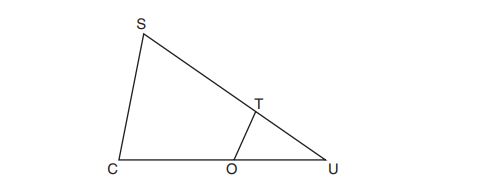
20. The ratio of similarity of to
is
. If
and
, then the length of
is
(1)
(2) (3)
(4)
21. In the diagram below, ,
,
,
, and
are chords of circle
,
is tangent at point
, and radius
is drawn. Sam decides to apply this theorem to the diagram: “An angle inscribed in a semi-circle is a right angle.”
Which angle is Sam referring to?
(1)
(2)
(3)
(4)
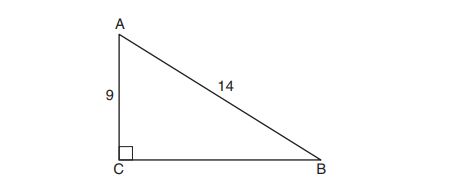
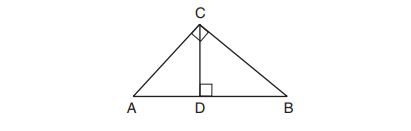
22. In the diagram below, is the altitude drawn to the hypotenuse
of right triangle
.
Which lengths would not produce an altitude that measures ?
(1) and
(2) and
(3) and
(4) and
23. A designer needs to create perfectly circular necklaces. The necklaces each need to have a radius of cm. What is the largest number of necklaces that can be made from
cm of wire?
(1)
(2)
(3)
(4)
24. In shown below, points
and
are on
and
, respectively. Segment
is drawn so that
.
If , and
, what is the length of
?
(1)
(2)
(3)
(4)